0

Hello all of you engineering geniuses. Awhile ago a very talented individual on here helped me work out the conceptual mechanics of this design. As you can see from the model, there is a lead screw assembly that pushes a rod forward which elevates the platform. The total travel is 0° to 60° (theta). The equation shown is the linear travel of "Xblock" as a function of theta. If you were to plot this function, you will see it is not quite linear. The terms, Wp, Ht, Hp, and Lrod are all constants. I am trying to determine an equation for angular velocity of the platform, which is actually decelerating as Xblock moves forward at a constant velocity. Of course the linear travel is easy enough, simply the rps of the motor x lead x time. The lead is 8mm but the lead and rps can be treated as constants. I could simply take the derivative of function, but it's a function of position as a function of another position, not time, so I'm not entirely sure where to go from here. 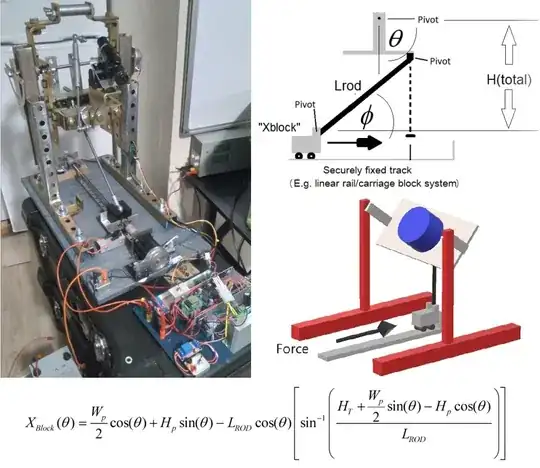concept

D Carson
  • 35
  • 5
  • looks like you can derive dx/dϑ directly from your equation (e.g. with Mathematica, or numerically if it makes your life easier) invert it to get dϑ/dx, multiply that by dx/dt to get dϑ/dt – Pete W Feb 14 '21 at 18:04

1 Answers1

1

As PeteW mentioned you can differentiate both sides of the equation with respect to t, and then solve for $\dot\theta(t)$.

If I done correct the calculations, you'll end up with

$$\dot\theta(t) = -\frac{X'(t)}{a(\theta(t)) + b(\theta(t))}$$

where:

  • $a(\theta(t))= -H_{p} \cos(\theta(t))+ \frac{1}{2} W_{P} \sin(\theta(t))-L_{rod} \arcsin\left(\frac{H_T-H_{p} \cos(\theta(t))+\frac{1}{2} W_{P} \sin(\theta(t))}{L_{rod}}\right) \sin(\theta(t)) $
  • $b(\theta(t))= \frac{\cos(\theta(t))}{\sqrt{1-\frac{\left(H_T-H_{p} \cos(\theta(t))+ \frac{1}{2} W_{P} \sin(\theta(t))\right)^2}{L_{rod}^2}}} \left(\frac{W_{P}}{2} \cos(\theta(t))+H_{p} \sin(\theta(t))\right)$
  • $X'(t)=\frac{2\pi n}{60} l_{thread}$: the velocity of the cart:
  • $n$ is the revolutions per minute [rpm]
  • $l_{thread}=8[mm]$ is the thtread size in [meters]

After, all the simplifications the angular velocity can be calculated as a function of $n [rpm]$, and $\theta [rad]$

$$\dot\theta(n, \theta) = -\frac{2\pi l_{thread}}{60(a(\theta) + b(\theta))}n$$

where:

  • $a(\theta)= -H_{p} \cos(\theta)+ \frac{1}{2} W_{P} \sin(\theta)-L_{rod} \arcsin\left(\frac{H_T-H_{p} \cos(\theta)+\frac{1}{2} W_{P} \sin(\theta)}{L_{rod}}\right) \sin(\theta) $

  • $b(\theta)= \frac{\cos(\theta)}{\sqrt{1-\frac{\left(H_T-H_{p} \cos(\theta)+ \frac{1}{2} W_{P} \sin(\theta(t))\right)^2}{L_{rod}^2}}} \left(\frac{W_{P}}{2}\cos(\theta)+H_{p} \sin(\theta)\right)$

NMech
  • 23,917
  • 2
  • 30
  • 72
  • Well look who it is! Seems like you are always the man for the job. You should be pleased to know that I used your original equation to derive a 3rd order polynomial (based on hard values for Hp, Wp, etc.) and am utilizing that in LabVIEW to achieve positioning. I'm getting great accuracy, precision, and resolution even with this model made of parts thrown together. I could have used that polynomial for these calculations but it's still a best-fit line, so some data points are off, albeit only by a few negilible milliseconds. Once again, amazing work. Thank you. – D Carson Feb 15 '21 at 15:23
  • Hi, First of all thanks for the kind words. Its my turn to say that your build is very impressive, and you have it fully instrumented. I am quite interested in how you control the Labiew.. do you use position control or do you control velocity? In any case, I wanted to remind you that, as you increase the velocity you will see greater differences, because the dynamic effects were not considered in the derivation. – NMech Feb 15 '21 at 18:56
  • https://imgur.com/VQ5nwrX – D Carson Feb 16 '21 at 18:47
  • https://imgur.com/LZ8P5RK – D Carson Feb 16 '21 at 18:48
  • https://imgur.com/m8NPapC – D Carson Feb 16 '21 at 18:48
  • https://imgur.com/wCBPWLE – D Carson Feb 16 '21 at 18:48
  • I'm not sure how to get images to show up in my comments like you are doing. Let me know if you can't see them. The velocity of the lead screw assembly remains constant, other than having it coded to accelerate/decelerate upon stopping points. 2.2rps is approximately equal to 4.1°/s angular velocity. But as you know, the velocity of the platform is not entirely linear, as it slows down as it moves up. A hard velocity requirement isn't a constraint of the system. – D Carson Feb 16 '21 at 18:57
  • From what I saw very quickly you have a command "go up" and "go down" and while the button is pressed, the cart moves. Is that right? The reason I am asking is because I am currently making the interface of a similar linear stage, where positioning is crucial. The problem was that I was not happy with the buttons (sometimes it was difficult to press them), so I opted to connect a game controller and control it trhough there. – NMech Feb 16 '21 at 19:02
  • Also I am not familiar with the library you are using... is it home brewed? – NMech Feb 16 '21 at 19:03
  • The system moves from the starting 0° point, to -8°,then 0°,10°,20°,30°,40°,50°,and 60°. At each stopping point, the operator is able to perform a fine adjustment. In the images linked I showed 10° as an example. In the LabVIEW case structure, "10 Degrees" is moving from 0° to 10°. The "Step10" state is the fine adjustment, where the platform can be moved with a resolution <0.1°. – D Carson Feb 16 '21 at 19:05
  • The first image is the code for acquiring motor driver current, optical encoder pulses, and Hall sensor output from a DAQ device. It is coded so the two position sensors must remain within a tolerance of each other, keeping each other in check essentially. Are you referring to the LINX (green) resources or the ULx (blue) for NI LabVIEW resources? The LINX is for motor control. ULx for the DAQ. LINX is a project by DIGILENT who is owned by National Instruments. They are available on LabVIEW community if you don't have other means of acquring them. – D Carson Feb 16 '21 at 19:08
  • Yes it responds accordingly to the up/down buttons. If you are saying you were having problems with unresponsive or lagging buttons, that could be a number of things but often some other process is running that causes a conflict/delay. Getting creative with the code to efficiently utilize memory can sometimes help. That happens pretty often with the stop button. People make code and want everything to stop when you press stop, but it will work much better if it's already coded to end processes at the right time, prior to pressing the stop button. – D Carson Feb 16 '21 at 19:46