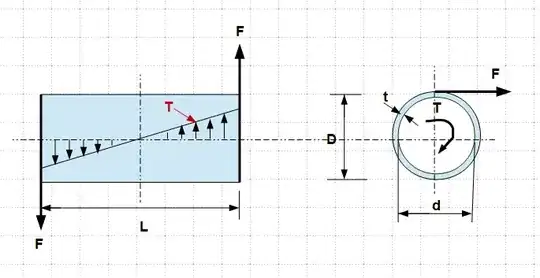
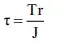I need to design a hollow drum that holds steel wire rope under tension. The wire rope gets pulled from both ends with a force of 200kN, it is wrapped around the drum 5 times. The outer diameter needs to be 1m and I was thinking of using S355 for this application.
My question is: How would I go about calculating the minimum wall thickness of the drum, as to withstand the ''crushing'' pressure of the wire wrapped around it?