8

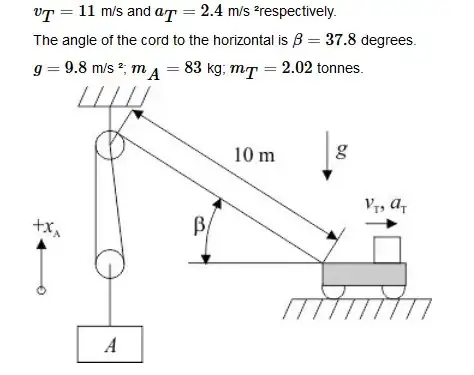
Have spent hours poring over this homework question but am having difficulty getting the right process going to solve the problem. I don't really know where to start, and I'd really be grateful if someone could show me the ropes (pun intended ^_^). There are two components to the question.

(a) What is the tension force $T$ in the cables at this instant (Newtons)

(b) What is the net horizontal thrust force required to produce the truck's motion? This includes drive force from the wheels, rolling resistance and air resistance.

The Problem

My (flawed, obviously) attempt at A went something like this:

  1. Draw FBD for block A

  2. Apply Newton's Second Law, where tension in cable is constant throughout its length $F_{y,A} = 2T-m_A\cdot g = m_A\cdot a_A$

  3. Length of cord is constant, so $L = -2X_A+X_T + C$, and $-2a_A+a_T = 0$, so the acceleration of block A is $\frac{1}{2}a_T = 1.2\text{ m/s}^2$.

  4. Rearranging equation from (2) provides $2T = m_A*g + \frac{1}{2}m_A\cdot a_T$, and then T = 456.5N.

Part B I struggle with altogether, because I don't have a clear process in my head to tackle the problem.

Edit~ A written attempt at a solution - Not sure how to factor in the angled a(T) as proposed...

enter image description here

Dave Tweed
  • 6,824
  • 1
  • 19
  • 34
Elisa Accordino
  • 81
  • 4
  • Do you have the static friction coefficients for those reaction forces? Did you draw a FBD for the truck? Seems odd, but in cases like these, you can usually assume air friction = 0. Get the X component of the Tension Force and then you have a simple Ftx(force of the truck) + the resistance forces in the X direction. [Maybe this will help, but your textbook should provide you with these](http://hpwizard.com/tire-friction-coefficient.html) – GisMofx Sep 02 '15 at 13:37
  • No friction coefficients :/ It's supposed to be simpler than it looks - not worth very many marks. I have attempted an FBD for the truck, however I wouldn't consider it to be correct, especially considering I couldn't manage a correct FBD for block A. I'm usually alright at FBD's, but my usual method doesn't seem to be working out. – Elisa Accordino Sep 02 '15 at 13:42
  • Post your FBD of the truck. You should end up with something like `TCos(b) = Tx = Ftx+Rair+Rrolling` - "plug and chug" – GisMofx Sep 02 '15 at 13:53
  • Also, you may want to double check your Tension Calculation. Your FBD for the Lower Pulley would be something like `FA = 2*T.` The Tension in your rope would simply be FA/2 or 406.7N - Draw a FBD for each pulley and remember tension is the same throughout the cable – GisMofx Sep 02 '15 at 14:08
  • The tension in the rope is not 406.7N. I'll rewrite my FBD attempts and upload them shortly. – Elisa Accordino Sep 02 '15 at 14:26
  • oops. I treated it as static. Isn't Block A `Acceleration = At*Cos(b)/2` ? So would Ftx = MtAt = TCos(b)+Freactions – GisMofx Sep 02 '15 at 14:40
  • @Elisa You're only mistake, as GisMofx points out, is that the rope is not accelerating along its length at $a_T$ because there is an angle between the truck's displacement and the rope's displacement. Take that angle into account to calculate the acceleration along the length of the rope ($a_T\cos(\beta)$) and you should have the correct answer. – Chris Mueller Sep 02 '15 at 14:43
  • I hastily added divided by 2, but it's just what @ChrisMueller has said. – GisMofx Sep 02 '15 at 14:48
  • Okay, just wrote out the "wrong" calculations, but I'll try again with your suggestions @ChrisMueller and @GisMofx! – Elisa Accordino Sep 02 '15 at 14:49
  • Have edited question with image of calculations as asked :) – Elisa Accordino Sep 02 '15 at 15:16
  • @Elisa, the second part of the problem should be straightforward after you have the tension. Think about the truck as a separate entity with the tension of the rope pulling back and the tires providing a force to push it forward. Without rolling and air resistance the equation is simply $m_Ta_T=-T\cos(\beta) + F_T$ where $F_T$ is the 'thrust force' applied by the engine. The air resistance will be a backwards (negative) force of the form $F_{air}\propto v_T^2$ and the rolling resistance will be a backwards (negative) force proportional to the weight of the truck $F_{rr}\propto m_Tg$ – Chris Mueller Sep 02 '15 at 17:13
  • Thanks @ChrisMueller - in my working I found F(T) to be negative, but I realize now that as it is a thrust it must be (overall) positive. Still cannot find T, I think this is either an issue with my FBD of block A or equation of constraint for the acceleration of the pulley cord - still unsure how to fix that/ set the necessary equations properly. – Elisa Accordino Sep 02 '15 at 23:11

1 Answers1

1

The cord from the truck to the first pulley is on a diagonal, so the length of that section does not increase linearly with the trucks motion:

$$L=-2X_A+\sqrt{{Y_t}^2+C^2}$$

Where $Y_t$ is the horizontal distance from the pulley to the truck, and C is the vertical distance. Defined by:$\frac{Y_t(t=0)}{\cos(\beta(t=0))}=\frac{C}{\sin(\beta(t=0))}=10m$

Differentiating with respect to time yields:

$$0=-2V_A+\frac{V_t\,Y_t}{\sqrt{Y_t^2+C^2}}$$

And differentiating a second time yields:

$$0=-2a_A+a_t\frac{C^2Y_t+{Y_t}^3}{({Y_t}^2+C^2)^\frac32}+\frac{C^2{V_t}^2}{({Y_t}^2+C^2)^\frac32}$$

From there one can solve for the acceleration of the block, and plug in.

Plugging in:

$$Y_t(t=0)\approx7.9m$$ $$C\approx6.1m$$ $$a_A(t=0)\approx3.2\frac{m}{s^2}$$ $$T(t=0)\approx540.6N$$

Interestingly there's a greater contribution to the acceleration from the angle of the cord changing due to the velocity (the ${V_t}^2$ term), then there is from the actual acceleration of the truck (the $a_t$ term). This makes sense if you think about how fast that truck is moving relative to the dimensions in the problem, and how relatively slowly the truck is accelerating.

Once one has the tension, the total thrust of the truck (ie the wheel trust minus all losses other than tension) will just be the net force in the horizontal direction plus the horizontal tension.

$$F_{net}=\text{Thrust}-T\cos(\beta)=m_t\,a_t$$

$$\text{Thrust}\approx 4825N$$

Rick
  • 1,295
  • 8
  • 23