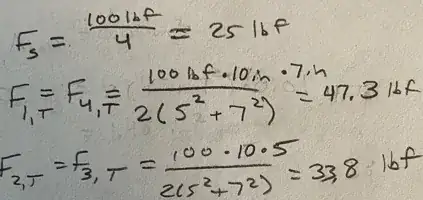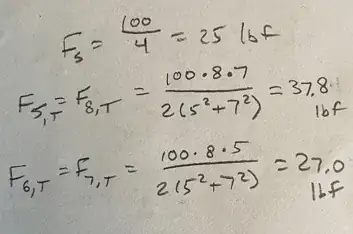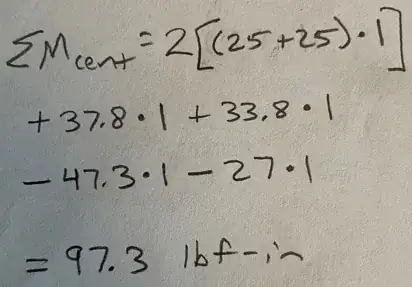Method 1 - Common Structural Design Approach
Assume the door is simply supported by the hinges on the jamb, and solving the reactions on the support hinges. The design shear on the screw is the resultant of T & V, which numerically equals the resultant of C & V.
For the purpose of design, you can stop here, since all screws must be the same size for the reason of economy, and with the understanding that the jamb side hinges are more critical than the door side hinges since they carry the loads passed from the centroid of the door to the door side hinges, then onto the jamb side hinges.
Let's see how this scheme works:
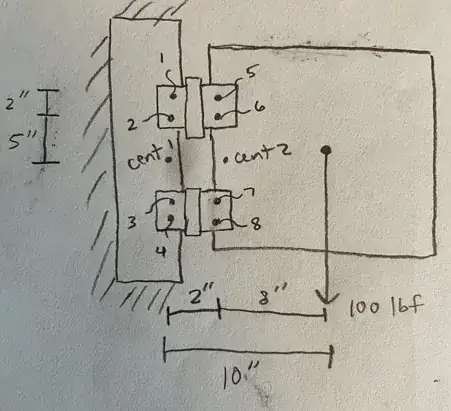
In the figure below, $\sum M = 0$, then $T = C = 100*10/12 = 83.33 lbs$; and $\sum Fy = 0$, and assume the two hinges share the same amount of the vertical load, that is $V = 100/2 = 50 lbs$.
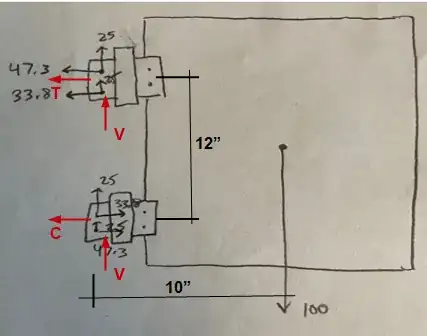
Now the forces on the upper hinge are as shown in the figure below. The component forces on a single screw are simply equal to one-half of the respective force in the vertical and horizontal directions ($F_V = V/2$ & $F_T = T/2$). Finally, the shear force on a single screw $R = \sqrt{F_V^2 + F_T^2}$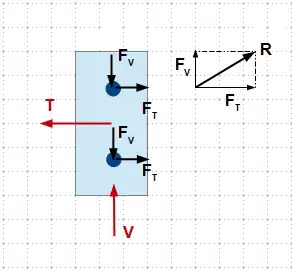
Method 2 - Exact Solution
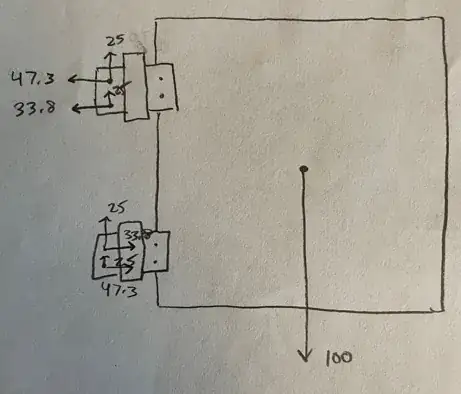
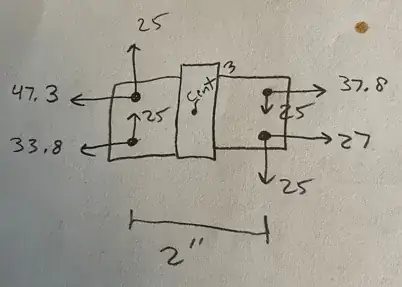
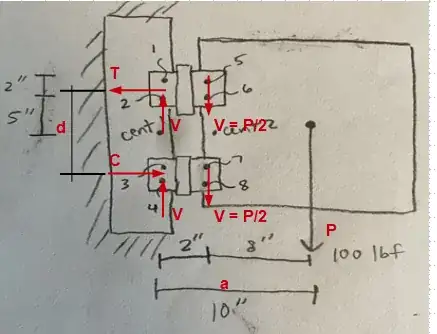
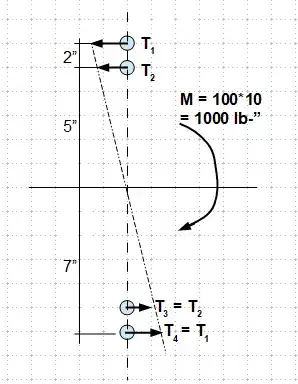
As shown in the figure below, you can solve the component horizontal forces using the exact method, which assumes a rigid bolt group subjects to externally applied moment/torque, and the stress of the screws are linear elastic.
Through the realization of $T_4 = T_1$, $T_3 = T_2$ and $T_2$ is proportional to $T_1$, you can solve the component force by $\sum T_i*a_i = M$. The most critical shear force thus is the combined horizontal and vertical shears of the outermost screws.
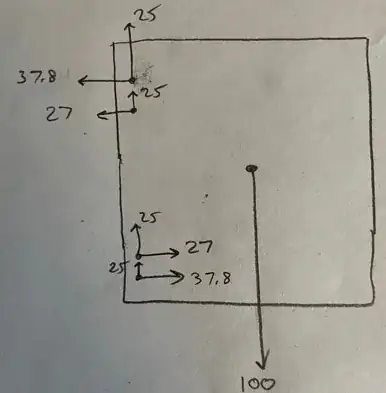
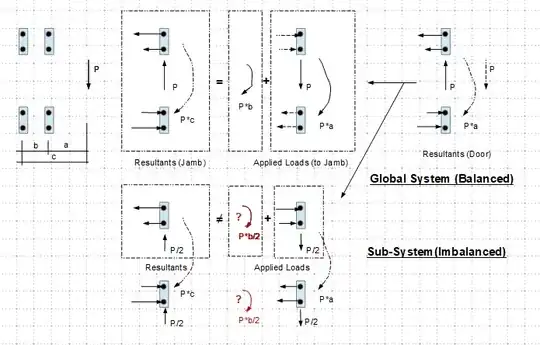
System Equilibrium Check - The system is in equilibrium, since $\sum F_x$, $\sum F_y$ and $\sum M$ about the center of origin "O" are all zero.
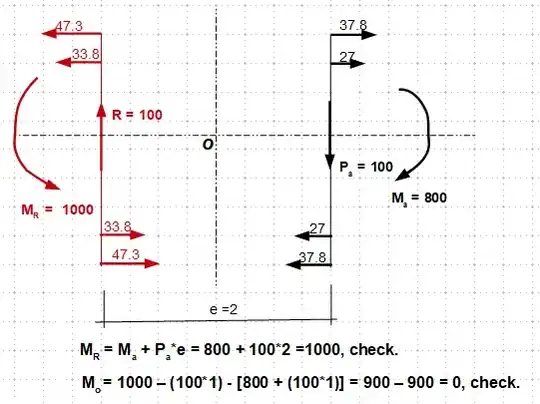
Note that you can't expect the unbalanced sub-system (the upper or lower pair) alone to be in equilibrium, because in which $\sum F_x \neq 0$ and $\sum M_{ctr} \neq 0$.
The sketch below demonstrates my last comment. Hope this helps.
Final THought
To further illustrate the concept of system balance, let's assume the door was supported on its right bottom corner, and the hinges on its left edge acting as another support, which subjected to a force of 100 lbs, the system is as the left figure shown in the sketch below.

Now we can analyze the upper pair of hinges separately, the respective forces are shown in the diagram on the right, and we note that while the entire system (which includes all four screws) is in the state of equilibrium, the sub-system does not (since $\sum F_x \neq 0$).
In a similar manner, let's imagine the hinge "A" is in place of the screw "A" and so on for hinges B thru D, then, through drawing a parallel with the note above, we realize why the pair of the upper hinges in your calculation ending in system imbalance.
Though I didn't check the number, I think your calculation and the results are theoretically correct, as there are indeed having unbalanced forces locally (sub-system), but will be balanced globally (full system).