Example
Since the rest of the answer is too long I will start with an example.
Imagine you could build a heat exchanger from wooden pipes. If you run through the liquid you would observe very little efficiency (i.e. the hot liquid would remain hot and the cold cold). There would be too little heat exchange, because the wood would not allow heat to pass through the material at any significant rate.
combined conduction and convection
You have to remember that the problem of heat transfer between the hotter fluid (h) and the cooler (c) is a combined conductivity and convection problem.
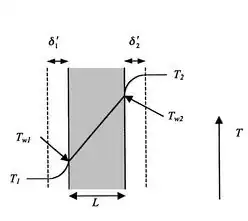
Figure Conducting wall with convective heat transfer (source: MIT thermodynamics)
Where:
- $T_2$ is the hotter fluid
- $T_1$ is the cooler fluid
- $\delta_1$, $\delta_2$ are the convective zones. I.e. the zone where the temperature in the fluid will change. This zone will change with the velocity and the viscosity and other geometric parameters
In those problem sometimes, the concept of thermal Resistance is introduced. Thermal resistance shows what is the energy per area for a degree of temperature difference. It is important to note that as the Thermal resistance increases, less heat energy is transmitted per temperature degree difference $\Delta T$ (or $\Delta T_{LMTD}$ to connect to the previous question)
In the above case, the thermal resistance is:
$$R= \frac{1}{h_1A} + \frac{L}{A \color{red}{k}} + \frac{1}{h_2A}$$
where:
- L is the thickness of the wall (pipe)
- A is the exchange area
- $h_1$ and $h_2$ the heat convectivity coefficient
- $\color{red}{k}$ heat conductivity coefficient
As you can see the thermal resistance is inversely proportional to the thermal conductivity. This means that when thermal conductivity of the pipe is high, then the thermal resistance is low.
Steady state of a heat exchanger
The problem with heat exchanger is that they come into too many flavors. Usually you encounter the parallel and the counterflow (but there are several others). Below is the example of those types of heat exchangers. In this image you can see the temperature difference
figure: Temperature difference along the length of the heat exchanger for different types of flows
In that image you can see immediately the problem. If you have a heat exchanger with a parallel flow you will have different temperature difference at different section of the heat exchanger (thus different heat transfer rates because the $\Delta T$ varies). (The same problem exists with the counterflow to a lesser extent.)
However, this is the temperature distribution of the steady state.
Transient state (short parenthesis)
The transient state is (in the simplest case) when the heat exchanger starts its operation. Then the fluid that passes can be assumed to have a uniform distribution (i.e. does not change with location).
However, the temperature distribution will change with time, and it will approach the steady state solution. It is obvious that during the transient state the heat transfer will be greater because the temperature difference will be greater compared to the steady state. So the bottom line is that, at the steady state there is the least heat transfer compared to all the transient states that led to it.
Putting everything together
From the previous paragraphs, I was trying to highlight that the steady state will have a temperature distribution along the length of the heat exchanger that should remain constant (wrt to time).
Therefore for a infinitesimally small portion along the length of the heat exchanger (with area A) the temperature difference can be assumed to remain constant wrt time. In that portion, the heat transfer rate can be assumed to be:
$$\dot{Q} = \frac{\Delta T}{R}$$
However as we've seen before as the thermal conductivity (k) increases, then thermal resistance R decreases, and as R decreases the heat transfer rate increases. That means that:
for increasing thermal conductivity (k), there is more heat transfer for the same temperature difference.
Since in the steady state the temperature difference is constant, the heat exchange will be dominated by the thermal resistance, and therefore it would be affected by changes in the thermal conductivity.
Why is the effect not pronounced in metals
The reason the heat conductivity effect is as not pronounced in metals is that because Thermal Resistance R is determined by the equation:
$$R= \frac{1}{A}\left(\frac{1}{h_1} + \frac{L}{\color{red}{k}} + \frac{1}{h_2}\right)$$
Then, the lowest of the $h_1$, $h_2$ and $\frac{k}{L}$ will have the dominating effect on the heat conductivity. Since usually $h_1$, $h_2$ coefficients are significantly lower than $\frac{k}{L}$ (unless L becomes too great), any change of thermal conductivity is not affecting affecting significantly the thermal resistance. (this is exactly the point mart's second paragraph is trying to raise).