TL;DR: I will expand on DKNguyen answer, which provides all the salient points. i.e. (my interpretation) the downforce is desirable to provide a better interface/grip between the car and the ground.)
Comparison of drag and lift coefficients for automobiles.
The following graph presents a comparison of drag and lift coefficients.
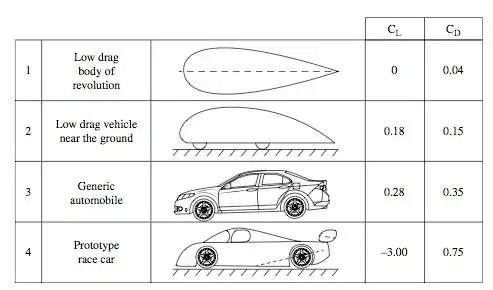
figure (source technicacuriosa
First of all notice the high value of drag $C_D$ on the prototype race car. You would expect it actually be lower than an average commercial car (It is not a spelling mistake!), and yet its over double.
Additionally, notice the value for the coefficient of lift $C_L$. Notice the negative value and fact that its an order of magnitude greater than a commercial vehicle.
*Short note on Lift on commercial (-non supercar-) vehicles: On of the reasons for the positive $C_L$, is the clearance below the vehicle. This makes the car loose grip and feel (sometimes) more like floating and become "wobbly" at high speeds (apologies the correct word doesn't spring to mind).
Aerodynamic Drag and Engine
Although covered in many other answers recently the top speed is when the aerodynamic drag is equal to the force that ends up on the wheels when they are driven by the engine. I've written this long description, because the force on the wheels changes depending on the speed (assuming a constant power).
$$P= F\cdot u \rightarrow F= \frac{P}{u}$$
This is summed up very nicely in a graph like the following (notice that the $\color{blue}{\text{blue curve}}$ is depended on $\frac{1}{u}$ which explains the hyperbolic shape):
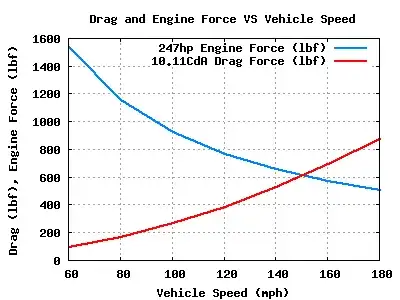
figure 2: Aerodynamic drag and force on the wheels (source: hogervorst)
The top speed is where the two curves meet.
increasing the Power of the car (and the limitations)
Arguably, since its possible to increase the engine car, this would shift the $\color{blue}{\text{blue curve}}$ further up.
The problem is that as the $\color{blue}{\text{blue curve}}$ shift up, so does the Force at which there is equilibrium. And that force is the force that the wheel should be able to act on the ground. Therefore, there is a limitation based on the how much traction force is possible for the tires to exert.
Traction force.
The traction force T can be approximated by the static friction law (not kinetic):
$$T = \mu \cdot N $$
Where:
- $\mu$ is the friction coefficient between the tires and ground (assume its constant)
- $N$ is the normal reaction to the ground. (Sometimes we forget that the normal reaction is not just weight.)
So this is where the Coefficient of lift comes into play. By increasing the coefficient of lift, effectively we can utilize better an engine with more horsepower.
Also keep in mind that the aerodynamic lift and drag have similar equations, i.e. :
$$F_D = \frac{C_D}{2}\rho\cdot A\cdot v^2 \qquad F_L = \frac{C_L}{2}\rho\cdot A\cdot v^2 \qquad $$
where:
- $F_D$ is the drag force
- $F_L$ is the lift force
- $\rho$ is the air density
- $A$ is the cross-sectional area
- $u$ is the velocity of the car
The point being, that: for a fixed surface/wing car increasing the drag has a proportional increase in lift (either upward or downward). The trick is to trim the car in such a way that optimises its performance.
Bottom line
For the cars you are considering, the engine power is so much that you'd probably only burn rubber is not for a significantly high downforce.
So - in that high horsepower scenario - the downforce is desirable to provide a better interface/grip between the car and the ground. This can help to:
- improve handling (the car sticks to the ground)
- improve acceleration (provide better traction)
- increase the top speed by utilising better any overkill in horsepower (if trimmed correctly).
Numerical Example
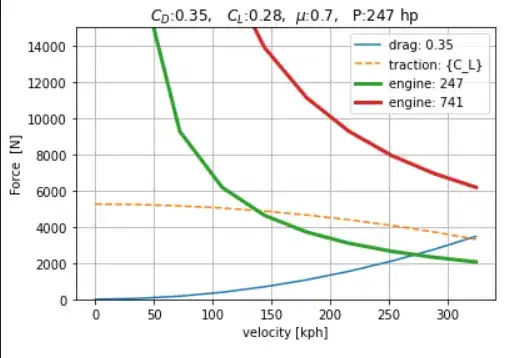
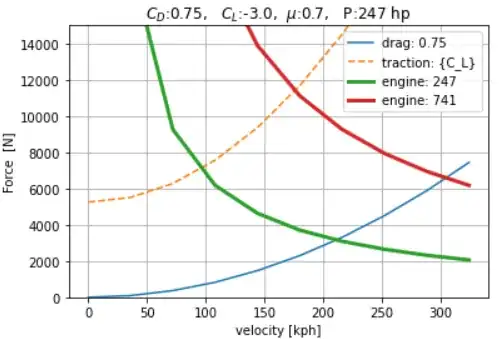
Assuming the values for the prototype car ($C_D=0.75$, $C_D=-3$), and $\rho=1.225 \frac{kg}{m^2}$ and $A = 2 [m^2]$, then the lift and drag values are presented in the graph below:
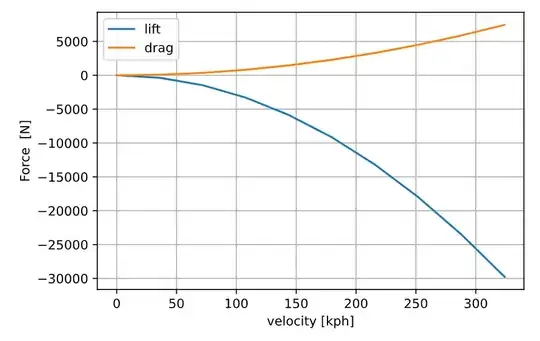
For 300 kph, (~ 185 mph), the downforce is about 30000 N. A car like that will between 7500 [N] and 15000 [N] so the normal reaction $N$, increases from $m\cdot g$ to respectively $5\cdot m\cdot g$ or $3\cdot m\cdot g$. This means that you can apply 3 to 5 times more force on the wheels.
Comparably, the drag will be twice that of a "normal" car, but there is still room to gain traction force.
You can see this in the diagram below, where 4 curves are plotted:
- the drag force
- the force on the tires from the engine for 247 hp
- the force on the tires from the engine for 741 hp
- the traction force limit (dashed line)
|
generic automobile |
prototype racing |
| $C_L$ |
0.28 |
-3.0 |
| $C_d$ |
0.35 |
0.75 |
| curves |
 |
 |
In the case of the generic automobile the excess hp will never affect the top speed, because there will not be enough traction (at high speeds the lift will reduce the reaction from the ground and therefore the traction).