1

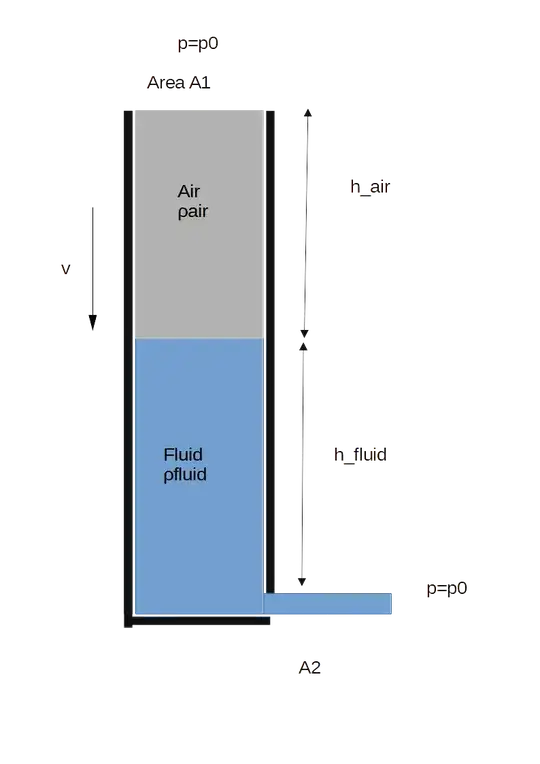
I want to calculate the efflux velocity for this open vessel with area $A_1$ with a small outlet with area $A_2$ as a function of time. The atmospheric pressure is $p_0$.

The vessel has height $h = h_{air} + h_{fluid}$ and is filled with a fluid. I want to take into account the velocity and potential head losses of the air. I am not interested in other losses.

An idea is to calculate the velocity starting from this equation.

$$(p_0-\rho_{air}g(h_{air}+h_{air} - z) -\frac{1}{2}\rho_{air}v^2)+\frac{1}{2}\rho_{fluid}v^2+\rho_{fluid}gz = p_0 + \rho_{fluid}\frac{A_1^2}{2A_2^2} v^2$$

I am in doubt as I don't know how to deal with the equilibrium at the interface between the fluid and the air. I know that in principle Bernouilli is not valid for a flow with two different fluids.

enter image description here

Wim Nevelsteen
  • 51
  • 6
  • 1
    The only efflux I see in this diagram is the water leaving the vessel volume through A2, so I don't understand why you are asking about the air flowing into the vessel. – J. Ari Sep 14 '21 at 12:50
  • I think that the air will have an impact on the pressure that the "water" feels, and that will have an effect on the velocity of the water. – Wim Nevelsteen Sep 14 '21 at 17:30
  • If the top of the vessel is always open to the atmosphere, then the pressure at the surface of the liquid will always be atmospheric pressure. This is essentially a tank draining problem that is addressed at the following links: https://ximera.osu.edu/ode/main/drainingTank/drainingTank https://www.youtube.com/watch?v=oIg2SxjF_Mg – J. Ari Sep 15 '21 at 19:25
  • But is there no pressure drop according to Bernouilli? – Wim Nevelsteen Sep 16 '21 at 00:17
  • The way you have the diagram, it makes me think that the area open to the atmosphere is large enough that the velocity needed for the air to fill in the volume of water leaving will be low enough to make the pressure loss negligible. – J. Ari Sep 16 '21 at 12:26
  • I agree that for practical purposes you can neglect it. The question was a conceptual question. I would like to know how I should take this loss into account in theory. – Wim Nevelsteen Sep 16 '21 at 18:40
  • 1
    You will want the inlet air volumetric flow rate to match the liquid volumetric flow out to avoid creating a vacuum greater than the vacuum rating of the vessel. You can calculate the air velocity in by dividing the air volumetric flow rate from above by A1. To find the dP due to that velocity, you'll need the proper correlation I wager. – J. Ari Sep 16 '21 at 21:23

0 Answers0