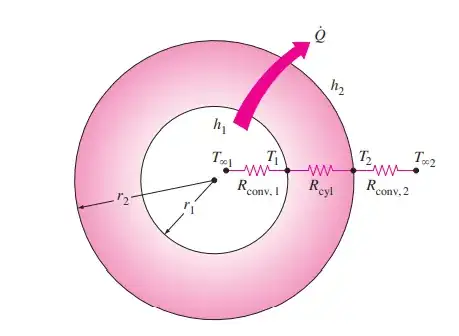
This is in regards to steady heat conduction taking place in a pipe.
Within the pipe a hot fluid flows and heat transfer first takes place via convection to the pipe and then via conduction within the pipe and then finally via convection from the pipe to the environment. As can be seen in the diagram, the author has taken the temperature at the inner surface of the pipe as constant $T_1$ as well as the temperature of the fluid is taken constant at $T_\infty1$.
However, I think when the fluid flows inside the pipe the surface temperature would be varying, it wont be constant at $T_1$. Similarly the average temperature of the fluid at every section will also not remain constant at $T_\infty1$(it will vary along the axial direction).
Is this only a sort of approximation? Is $T_1$ the average of the surface temperatures along axial direction and $T_\infty1$ the average of average fluid temperatures at cross sections along the pipe?
Excerpt from the book - https://drive.google.com/file/d/1WaBp4I-Nbx902G4stCCdRb01ZrDb_lLo/view?usp=sharing