Q: Could you siphon an 10 meter tall water column?

Question

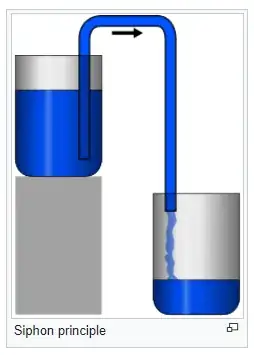
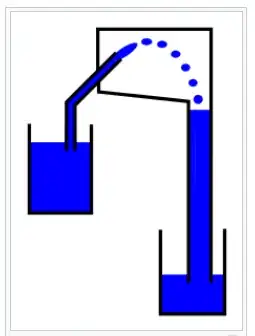
This question might be better suited for this stack. In the physics stack, I posted about a question about siphoning. https://physics.stackexchange.com/q/677102/259268

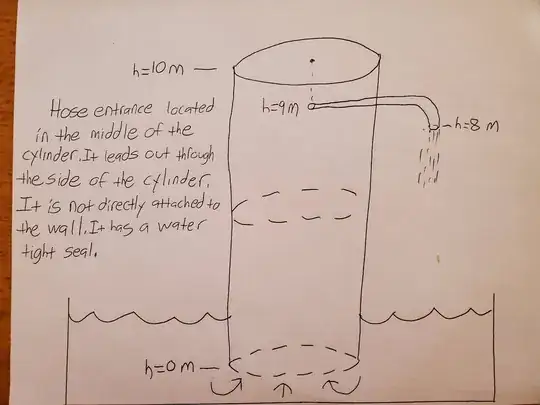
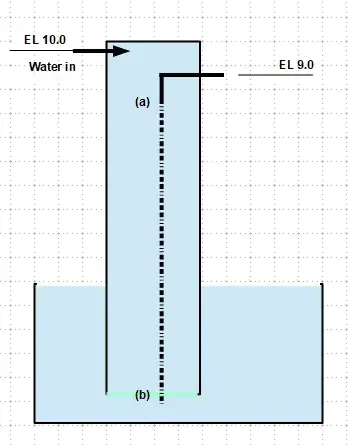
An 10 meter tall cylinder is sitting in a infinite pool of water. It has supports on the bottom attached to the base of the pool to maintain its vertical position. The top of the cylinder is closed and the bottom is open to the water. The bottom of the cylinder is not exposed to air and is submerged. There is a hose located 1 meter below the top of the cylinder which leads through the wall of the cylinder. The hose entrance is at a higher elevation (~9 m) than the hose exit (~8 m). Currently the hose exit is closed.

Water fills the cylinder and hose combination (the air is released, there is no air in the entire setup, only water). The atmospheric pressure outside the cylinder(and hose) and the properties of water allows for the 10 meter height of the water column. Suddenly the hose exit opens, starting the siphon process. Water drops 8 meters into a water turbine sitting level with the surface of the pool. Beneath the turbine is just an extension of the pool that the cylinder also occupies.

As the water falls from the hose exit, it starts pulling water from the top of the cylinder. The open bottom of the cylinder starts pulling water from the pool. The water goes through the turbine and re-enters the pool. The flow of water through the cylinder is continuous as it can not drain the entire pool of water.

I am more willing to know your thinking on this matter, especially will the reservoir be drained if its bottom is lower than the point of discharge. — r13, Dec 03 '21 at 16:44
The reservoir of water could be the ocean (near infinite source of water). The base of the cylinder could be submerged at a depth of 1 meter (or make it 2 meters). Once the hose starts siphoning from the top of the cylinder, wouldn't it continuously suck up water from the base (as long as no air enters). If the flow is continuous, you could design a system where the water drops into a water turbine and then returns to the ocean. — , Dec 03 '21 at 16:49
Side note: It has been shown that siphons work in a vacuum. The idea is that the water itself has strong cohesive forces between the molecules. The wiki article listed by Tiger calls it cohesion tension theory (similar to how xylem in plants pull up water). The water at the end of the hose literally pulls the water behind it creating a flow. Similar to a chain fountain. https://en.wikipedia.org/wiki/Chain_fountain — , Dec 03 '21 at 17:28
I know how the siphon works, my question was really to show that your setup is unclear and the prediction (reservoir drained) seems up to the setup and other conditions. You should consider updating your question and understanding to be more clear because there are a lot of "ifs". — r13, Dec 03 '21 at 19:02
Apologies R13, I was not very clear in my explanation. I made some changes. — , Dec 03 '21 at 19:25
"*If the flow is continuous, you could design a system where the water drops into a water turbine and then returns to the ocean.*" You seem to be trying to invent a perpetual motion machine. They're not possible. You can't win. You can't even break even. You are asking a system to take water from one level and discharge it at a higher level. That can't happen with a siphon or any other system unless you **add** energy. — Transistor, Dec 03 '21 at 19:57
Regarding to the added sketch, pls excuse my ignorance, how could the siphon to occur when the water elevation drops below 9 m? — r13, Dec 03 '21 at 20:31
Air can only enter the cylinder from two ways. The hose exit outside or the bottom of the cylinder. There is no air in the entire cylinder, water reaches the top. There is a meter of water above the hose entrance in the middle of the cylinder. I was thinking that this could start a siphon. Since the water would be flowing out of the hose, it would prevent air from entering through the hose exit. I thought this would cause water to be pulled up from the bottom of the cylinder and not collapse the water column. — , Dec 03 '21 at 20:37
According to my understanding, the siphon needs initial suction, then the flow will continue through capillary action (correct me if I am wrong), which in turn needs a continued path. Where is the uninterrupted path for flow in your sketch? — r13, Dec 03 '21 at 20:40
In my idea, the hose exit suddenly opens causing whatever water in the hose (on the outside) to be pulled down by gravity. As gravity pulls the water at the hose exit, I was thinking that would create the suction necessary to start the flow. — , Dec 03 '21 at 20:44
(1) Having the open end of the hose in the edge or centre of the cylinder doesn't make any difference. Pressure difference depends on **height only**. (2) Your `h = 0 m` is in the wrong place. It should be at the surface of the water as in my diagrams. Again it's the **difference in height between inlet and outlet** that matters and the inlet in your diagram is the open surface of the tank. (3) It doesn't matter how much water is above the outlet. (4) Having a hose go from the tank up to 9 m and back to 8 m gives you exactly the same thing (with maybe slightly more fluid friction resistance). — Transistor, Dec 03 '21 at 20:51
"*As gravity pulls the water at the hose exit, I was thinking that would create the suction necessary to start the flow.*" No, 10 m of water gives a pressure of about 1 bar (1 atmosphere). Let's say you have 7 m between the surface of the tank and the top of the hose and 1 m between the top of the hose and the outlet. When you open the valve you now have 0.7 bar suction on the left side of the hose and 0.1 bar suction on the right. Which way do you think the water will flow? — Transistor, Dec 03 '21 at 20:56
My misunderstanding was that the pressure at the hose entrance was dependent only on what was above it. I thought because the cylinder was closed on top that atmospheric pressure was counteracted by the cylinder. Which lead me to believe that the base of the water column in the cylinder had a higher pressure than the water at the top.. Your explanation clears this up. Thanks for answering my little thought experiment. — , Dec 03 '21 at 21:06
No problem. The fact that you were going to get energy for free should have set off an alarm bell in your head. Tip: if you want to "ping" someone so that they get an inbox notification you have to use `@username` with no spaces (even if there are some in the username) in your comment. Don't forget to accept an answer if your question has been solved. — Transistor, Dec 03 '21 at 21:22

score 2 · Answer 1 · answered Dec 03 '21 at 15:02

2

Siphons are limited by atmospheric pressure.

The exact why of this is a bit complicated, and the statement isn't quite correct, but we are right at the limit. Other factors are the liquid's vapor pressure, its characteristics, and the tube itself.

A 10 meter siphon must overcome the weight of 10 m of water.

We'll do this in both SI & Imperial units.

10m water = .098 MPa. Just under atmospheric at sea level

393.7 in water = 14.2 psi

answered Dec 03 '21 at 15:02

Tiger Guy

5,369
6
17

Thanks for the response. But why would the siphon need to overcome the entire water column? For example, if the entrance of the hose is 1 meter below the top, wouldn't the pressure be much lower? – Dec 03 '21 at 15:08
I don't know what "siphon near the top" means. A siphon is defined by the height of the water column. I'm also unclear reading it again how exactly you "formed" a 10m water column. Did you draw a vacuum on the top? – Tiger Guy Dec 03 '21 at 15:13
Sorry for that. The idea I was thinking of is a cylinder with only one opening with a height of 10 meters. The bottom of the cylinder is open but not the top (the bottom is in a pool of water). The water column reaches the top of the cylinder and there is no air. The hose is then inserted into the top of the cylinder and then siphoned out. I'm confused if the siphon is located near the top of the cylinder, wouldn't the pressure be less than 10 meter equivalent. (The hose is also full of water with no air). – Dec 03 '21 at 15:16
drawing water from below the top would look like a shorter siphon, so you should be fine. – Tiger Guy Dec 03 '21 at 16:23
Okay, now if the siphon works, how about this. The end of the hose is at a height of 9 meters. An 9 meter drop means the water is traveling at 8.25 mph (~13.3 km/h). Couldn't you put a water turbine at the base and generate electricity? The water could then return to the reservoir and get sucked up the cylinder repeatedly. – Dec 03 '21 at 16:31
a siphon only works with a height differential. You can't siphon water back to the reservoir without a pump. – Tiger Guy Dec 03 '21 at 16:54
Lets call this an idealized version. The entrance of the hose at the top of the cylinder is at height = 10 m. The end of the hose on the outside of the cylinder is at a height = 9 m (or make it height = 8 m). Doesn't that satisfy the conditions for a siphon to work? – Dec 03 '21 at 16:57
the pressures have to work. In this case, the flow would be back into the siphon, not out of it. Something has to provide the motive force to get the water to flow up your 10M column. – Tiger Guy Dec 03 '21 at 17:03
Let us [continue this discussion in chat](https://chat.stackexchange.com/rooms/132018/discussion-between-doug-and-tiger-guy). – Dec 03 '21 at 17:10
1

+1 THIS. This was my exact line of thinking when I saw the question and the "10-meter" stipulation. It might just barely work--on a high barometric-pressure day. On a stormy (low pressure) day, it might not work, because there would be insufficient atmospheric pressure to push the water over the peak. With insufficient pressure, you would just be left with a vacuum in the line at the top, and this would not siphon very well. – Polyhat Dec 05 '21 at 12:53

Transistor · Accepted Answer · 2021-12-03T19:43:15.003

0

A diagram in your question would be a big help. I think you are describing (a) above.

If you open the valve at the end of the hose at the 9 m level the weight of the 10 m water column will collapse the water column into the tank and suck all the water out of the hose as fast as the air can flow through the hose.

For a siphon to work the outlet must be below the level of the water exposed to atmospheric pressure - the surface of your tank in this case.

Note that your cylinder doesn't make any difference to just using a hose as shown in (b). The ΔP (delta-P / difference in pressure) between the tank surface and the pipe outlet will be the same regardless of the diameter of the column.

edited Dec 03 '21 at 19:43

answered Dec 03 '21 at 19:36

Transistor

9,424
2
19
30

Sorry for that. But your diagram is basically what I was describing in the question. The one I posted on the physics stack is slightly different where the shape is a sombrero (cylinder in the middle). Where water is sitting on top of the sombrero forcing down the structure into the pool. I was thinking that the buoyancy would support the water column. Just saw your second diagram. If the hose is not directly on top, but on the side of the cylinder at height = ~9 m, would that change anything? I really appreciate your help. Thanks again – Dec 03 '21 at 19:44
Lost the chance to edit the last comment to add one thing. The hose entrance is not directly attached to the cylinder. Its located in the middle of the cylinder, in the water column. – Dec 03 '21 at 19:52
Picture >> words. Add it to your question. – Transistor Dec 03 '21 at 19:53

r13 · Answer 3 · 2021-12-03T20:47:12.763

0

The sketch is to help you to clear up your question. You should identify where the hose is terminated - (a) or (b)? Please feel free to copy and edit the sketch to match your thought.