0

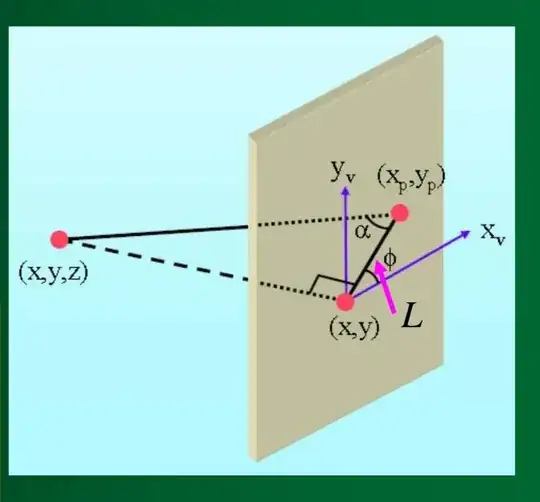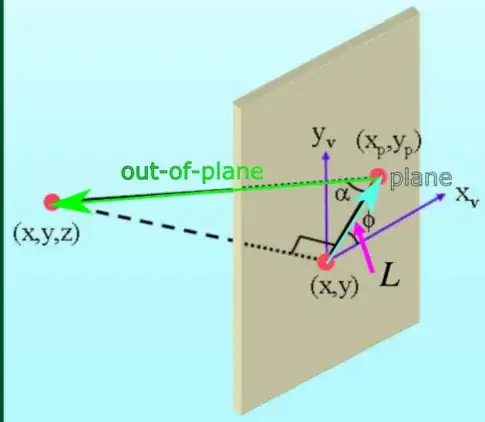
We know that in Oblique Parallel Projection Point $(x,y,z)$ is projected to position $(x_p,y_p)$ on the view plane.Projector (oblique) from $(x,y,z)$ to $(x_p,y_p)$ makes an angle $\alpha$ with the line (L) on the projection plane that joins $(x_p,y_p)$ and $(x,y).$ Line $L$ is at an angle $\phi$ with the horizontal direction in the projection plane.See this image1: enter image description here

And in Oblique Parallel Projection Angles, distances, and parallel lines in the plane are projected accurately.For example see below image2:enter image description here

My question is where is the angle $\alpha$ in image2, I mean I see the angle $\phi$ on the image , so where is $\alpha$ in that image to understand better?

N. B:1 -- I am following Hearn and Baker book which screenshot like this.

N. B. -- I want to understand just intuition in easy way rather than details.

Sahitto
  • 113
  • 6
  • Which page have you got to? – Solar Mike Dec 04 '21 at 21:32
  • @Solar it has 315 in Hearn and Baker book. – Sahitto Dec 04 '21 at 21:35
  • I think it is the angle between the -Zv axis and +Yv axis, which is 90 degrees in this case. – r13 Dec 04 '21 at 22:31
  • @r13 could you draw the image and level the $\alpha$ where is exist in the image.. – Sahitto Dec 04 '21 at 22:37
  • It is the angle in between the horizontal baseline and vertical line on the Yv, Zv plane. – r13 Dec 04 '21 at 22:52
  • Cross-posted: https://gamedev.stackexchange.com/q/198224/82314, https://engineering.stackexchange.com/q/48585/7678. Please [do not post the same question on multiple sites](https://meta.stackexchange.com/q/64068). – D.W. Dec 30 '21 at 20:05

2 Answers2

2

The angle $\alpha \ $is the angle of projection, meaning it has no shadow on the plane to be shown or measured.

However, if we know the length, L1, as shown on the figure and measure its projection from the figure, l1, then:

$$\pi/2 -\alpha=arctan(l_1/L_1), \quad \alpha=\pi/2-arctan(l_1/L_1)$$

.

angle of projtn

i apologize for poor sketch, but it conveys the message. angle phi image

kamran
  • 21,714
  • 2
  • 18
  • 38
  • it's the right-side view of cube or front view? You treat $a$ as $\alpha$? – Sahitto Dec 05 '21 at 05:51
  • it's the right side view. you need to click on the figure and enlarge it. yes i treat a, as alpha cause my sketch up is limited font. – kamran Dec 05 '21 at 06:31
  • I have one request could you show the whole image where original image projects to projected image with angle levelling? I will be helpful to got felt better as for beginner. – Sahitto Dec 05 '21 at 07:07
  • yes. its late here. I do it tomorrow. but basically its going to be too busy. the concept it L1 and its image l1 are the sides of triangle. but i do it tomorrow. – kamran Dec 05 '21 at 07:11
  • Thank you kamran. Hats off to you. And kindly you mention $\alpha$ and $\phi$ – Sahitto Dec 05 '21 at 07:24
  • Could you elaborate little bit-"it has no shadow on the plane to be shown or measured"? – Sahitto Dec 05 '21 at 12:07
  • @Ponting, I have lost my cloud sketch to edit it, but I will find it. By no shadows mean like drafting three views. The front view has no trace of the side plane or sidelines, only lines parallel or slanted to the view. As to angle $\phi$ it remains the same in the projected image. If you imagine a prismatic pentagon projected all the angles project the same 108 degrees. – kamran Dec 05 '21 at 20:38
1

enter image description here

  • The green arrow is the out-of-plane vector
  • the light blue arrow is the plane vector

Calculation of $a$ angle

If you got the coordinates $x,y,z$ and $x_p,y_p,0$ then the most generic way to use is through the dot product and the inverse cosine.

I.e.

  • the vector in the projection plane will have direction:

$$v_{plane} = \begin{bmatrix} x-x_p\\ y-y_p\\ 0\end{bmatrix}$$

and the unit direction vector would be:

$$e_{plane} = \frac{1}{||v_{plane}||}\begin{bmatrix} x-x_p\\ y-y_p\\0\end{bmatrix}=\frac{1}{\sqrt{(x-x_p)^2+ (y-y_p)^2}}\begin{bmatrix} x-x_p\\ y-y_p\\ 0\end{bmatrix}$$

Similarly, the out of plane vector is:

$$v_{out} = \begin{bmatrix} x-x_p\\ y-y_p\\ z\end{bmatrix}$$

and the corresponding unit direction vector would be:

$$e_{out} = \frac{1}{||v_{out}||}\begin{bmatrix} x-x_p\\ y-y_p\\z\end{bmatrix}=\frac{1}{\sqrt{(x-x_p)^2+ (y-y_p)^2 + z^2}}\begin{bmatrix} x-x_p\\ y-y_p\\ z\end{bmatrix}$$

The dot product of the unit vectors would be:

$$e_{out} \cdot e_{plane} = \frac{1}{\sqrt{(x-x_p)^2+ (y-y_p)^2 + z^2}}\begin{bmatrix} x-x_p\\ y-y_p\\ z\end{bmatrix}\cdot \frac{1}{\sqrt{(x-x_p)^2+ (y-y_p)^2}}\begin{bmatrix} x-x_p\\ y-y_p\\ 0\end{bmatrix}$$ $$e_{out} \cdot e_{plane} = \frac{( (x-x_p)^2 + (y-y_p)^2 )}{\sqrt{((x-x_p)^2+ (y-y_p)^2 + z^2) ((x-x_p)^2+ (y-y_p)^2)}} $$

$$e_{out} \cdot e_{plane} = \frac{\sqrt{ (x-x_p)^2 + (y-y_p)^2 }}{\sqrt{(x-x_p)^2+ (y-y_p)^2 + z^2 }} $$

At the same time:

$$e_{out} \cdot e_{plane} = ||e_{out}|| \cdot ||e_{plane}|| \cdot \cos(a)= 1\cdot 1\cdot \cos(a) = \cos(a) $$

therefore:

$$\cos(a) = \frac{\sqrt{ (x-x_p)^2 + (y-y_p)^2 }}{\sqrt{(x-x_p)^2+ (y-y_p)^2 + z^2 }} $$

$$a = \arccos\left( \frac{\sqrt{ (x-x_p)^2 + (y-y_p)^2 }}{\sqrt{(x-x_p)^2+ (y-y_p)^2 + z^2 }}\right) $$

(PS: please check the derivation for any mistakes/errors, because the final equation seems a bit too elegant)

Calculation of $\phi$

Calculation for $\phi$ angle can be expressed by the same equation but you can select a point on the x axis e.g. $(x, y, z) = (1,0, 0).$

In that case the equation will have the following form:

$$e_{out} \cdot e_{plane} = \frac{1}{\sqrt{(x-x_p)^2+ (y-y_p)^2 + 0^2}}\begin{bmatrix} x-x_p\\ y-y_p\\ 0\end{bmatrix}\cdot \begin{bmatrix} 1\\ 0\\ 0\end{bmatrix}$$

$$\phi = \arccos\left( \frac{x-x_p}{\sqrt{(x-x_p)^2+ (y-y_p)^2 }}\right) $$

NMech
  • 23,917
  • 2
  • 30
  • 72
  • could you show the image with projection and after projection with Projector and angle $\alpha$ and $\phi$, by which I can understand easily. – Sahitto Dec 05 '21 at 08:57
  • apologies, instead of $\phi$ I should have written $a$. I will correct it later, since I am out on a family excursion. – NMech Dec 05 '21 at 08:59
  • OK thank you.. Please do it as soon as possible. – Sahitto Dec 05 '21 at 09:01
  • the out of plane vector" mean and why z is present here? – – Sahitto Dec 05 '21 at 14:00
  • 1
    The "out of plane" refers to the vector which does not exists within the plane you see in the image. It is the vector connecting $(x,y,z)$ to $(x_p, y_p)$. The plane vector is the one connecting $(x,y) $ to $(x_p, y_p)$. – NMech Dec 05 '21 at 14:12
  • How you got $$e_{out} \cdot e_{plane} = \frac{1}{\sqrt{(x-x_p)^2+ (y-y_p)^2 + 0^2}}\begin{bmatrix} x-x_p\\ y-y_p\\ 0\end{bmatrix}\cdot \begin{bmatrix} 1\\ 0\\ 0\end{bmatrix}$$ in last paragraph and why you multiplying with \begin{bmatrix} 1\\ 0\\ 0\end{bmatrix}? – Sahitto Dec 05 '21 at 14:45
  • 1
    It's a similar process to the above. I'm finding the able between the in plane vector and the unit vector of the X axis. – NMech Dec 05 '21 at 14:53
  • could I ask when you provide the full image of projection with projector with angle? – Sahitto Dec 06 '21 at 07:20
  • I want to see 12 edges of original image projected to view plane with projected and angle $\alpha, \phi$ – Sahitto Dec 06 '21 at 08:30
  • still I am waiting for your image. – Sahitto Dec 06 '21 at 16:37
  • Το be honest I am not sure what is it that you are after in the image. I understand that you want to see the 12 edges of a cube, but I am not sure the camera position, or the cube position and size. – NMech Dec 06 '21 at 18:08
  • you could take any cube position, It's not mandatory . Necessary is levelling the the angle $\alpha, \phi$. Please help me to understand. – Sahitto Dec 06 '21 at 18:22