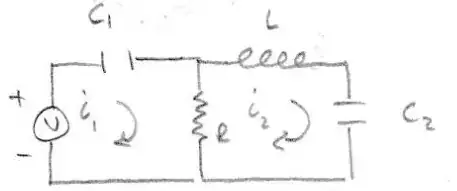
I have been attempting to model the following circuit using KVL and Simulinks:
Applying KVL generated these coupled differential equations:
$$ 0 = -V + \frac{q_1}{c_1} + R ( \frac{dq_1}{dt} - \frac{dq_2}{dt} ) $$
$$ 0 = -R ( \frac{dq_1}{dt} - \frac{dq_2}{dt} ) + L \frac{d^2q_2}{dt^2} + \frac{q_2}{c_2} $$
Rearranging,
$$ \frac{dq_1}{dt} = \frac{V- \frac{q_1}{c_1}}{R} + \frac{dq_2}{dt} $$
$$ \frac{d^2q_2}{dt^2} = \frac{R ( \frac{dq_1}{dt} - \frac{dq_2}{dt} ) - \frac{q_2}{c_2}}{L} $$
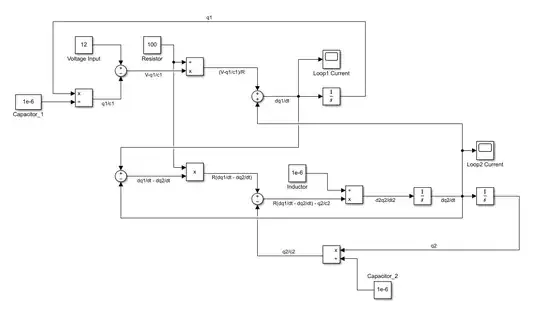
From here it seems straightforward to implement these equations using block diagrams in Simulink:
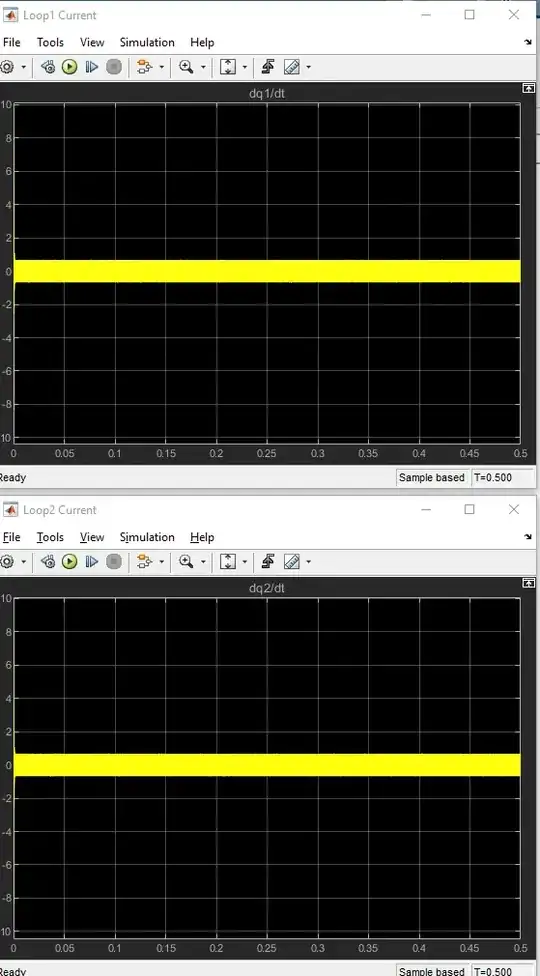
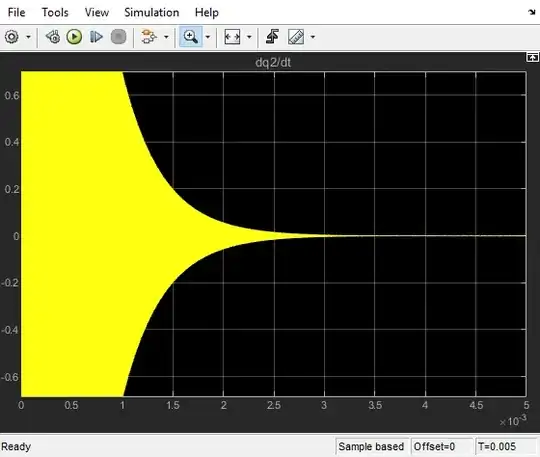
However the output is oscillatory in the extreme and requires very small step sizes to even resolve for values of V=12, R=100, C1=1e-6, C2=1e-6, L=1e-6.
I've played with other values for V, L, and C1/2, and am met with varying amplitudes of the oscillation, but the output loop currents never settle in the way that I believe they should.
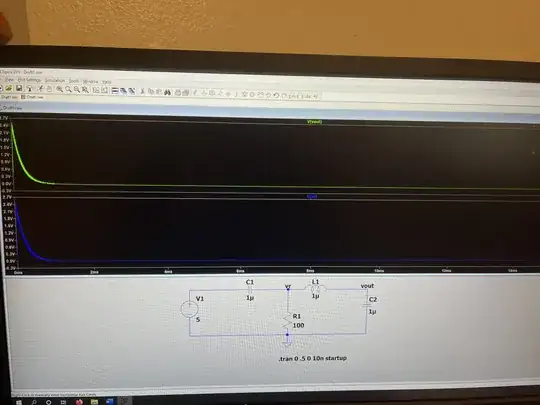
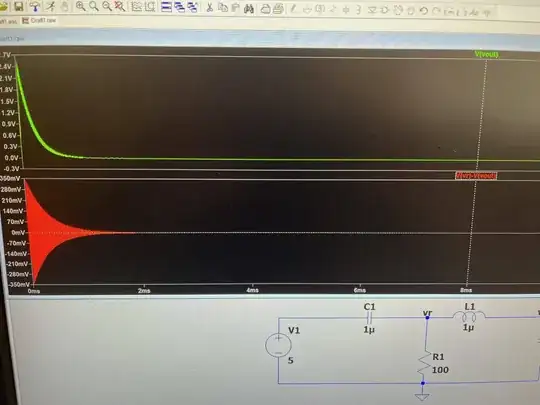
An LTSpice simulation of the circuit shows:
Which shows the inductor voltage ringing before settling to zero. This does not occur in Simulink, and I think this is why: the step size is too large, and thus the oscillation tricks Simulinks into performing non-representative arithmetic.
When I reduce the step size (and zoom in on the transient behavior):
This is still extremely oscillatory. Is my intuition that this shouldn't happen correct? Is Simulink simply not a good tool for this kind of problem?