Entrainment Speed in Ball Bearing

Question

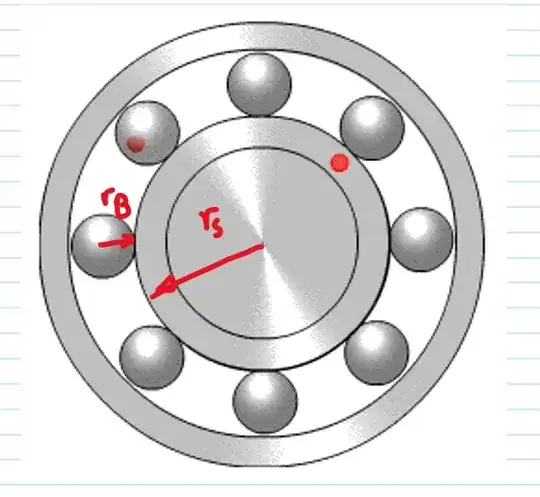
Assuming no slip between the inner race and the outer race of a ball bearing, what is the entrainment speed between the balls and the inner race? The inner race is rotating at $\omega_i$ and the outer race is fixed, $\omega_o = 0$, as shown below:

I know the entrainment speed is

$$ \bar{v} = \frac{1}{2}(\vec{V_1} + \vec{V_2}) - \vec{V_0} $$

I am having difficulty in calculating the velocity of the balls compared to the inner race using cross products and understanding how this relates to the entrainment speed equation.

The inner race has radius, $R_i$

The outer radius has radius, $R_o$

The balls have radius, $r$

Answer 1

I assume by entrainment speed you mean the velocity that the balls are moving along between the outer and the inner ring (I've only encountered entrainment with relation to fluid transport so I am 100% sure if that is that you are after).

Assuming the radii of the shaft ring and the ball are $r_s$ and $r_B$ respectively, (see image below)

Then, the point of the ball touching the ring should move with speed 0.

The point of the ball touching the shaft should move with a speed of $\omega_i r_s$.

Therefore there is a rigid ball that is moving with 0 at one end of the diameter and $\omega_i r_s$ on the other.

So:

• the speed at the center of the mass of the ball should be equal to $v_B = \frac{\omega_i r_s}{2}$ and
• the angular velocity of the ball should be $\omega_B = \frac{v_b}{r_B}= \frac{ r_s}{r_B}\omega_i $