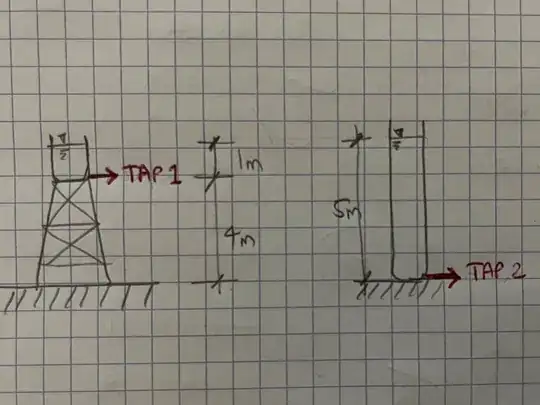
If I had two tanks of equal diameter, and one was was shorter but elevated, but the other was taller but sitting on the ground, which tap (with both taps connected to the bottom of the two tanks) would produce water with higher pressure? In this example, I am assuming the initial surface of the water in both tanks is at the same elevation.
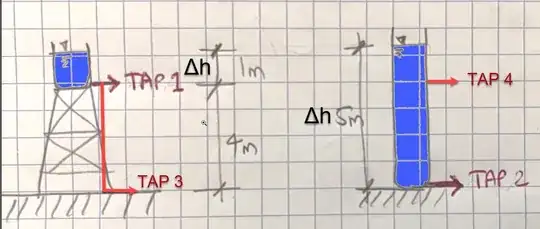
I think the taller tank (TAP 2 in my image) will produce more pressure (at least until the water surface depth matches the depth in the elevated tank/TAP 1 in my image, i.e., after 1 meter of water is drained). In other words, I think the additional weight of water in the taller tank would add more pressure to the pressure resulting from gravity (height). However, I am unable to back this up using formulas, since the Pressure Formula (P=pgH) only has Height has the major variable. How do we account for additional pressure as a result of the weight of water above a point/tap?