1

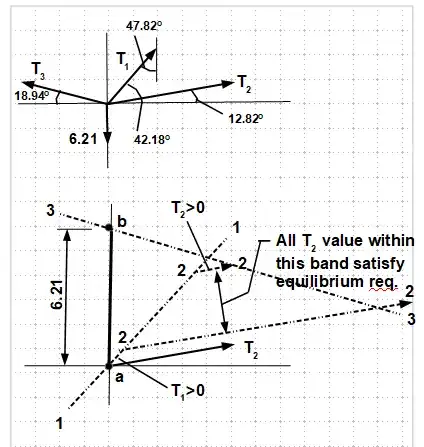
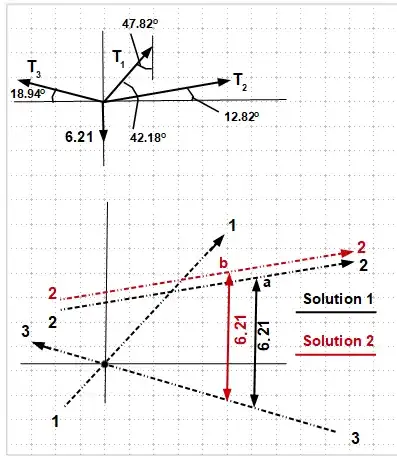
This problem is related to my previous question on the generalized Lami's theorem. I would like to see how you solve this problem and compare with my solution. My motivation for this problem is that I have not seen A SINGLE problem of this type on the internet that considers a 4-force system in static equilibrium. All the problems that I have seen consider 3 forces and those that consider 4 never ask for three unknowns, but offer more information in a way that can be solved by vector components. How do you solve this problem using vector components? I apologize for the ugly problem.

enter image description here

Note: The cable for T2 only hangs from the vertical line, NOT the horizontal.

Emmanuel José García
  • 133
  • 6

1 Answers1

1

The graphic diagram below shows there are infinite solutions (non-unique) to this problem.

Steps:

  1. Draw the gravity load to scale and mark the ends "a" and "b".

  2. Draw a construction line parallel to the vector $T_1$ from point "a".

  3. Draw a construction line parallel to the vector $T_3$ from point "b".

  4. Now make a line parallel to the vector $T_2$, but, what is the unique line length required to close the vector loop???

enter image description here

Let's try another sequence to draw the vector loop.

  1. Draw a line (3-3) parallel to $T_3$.

  2. Draw a line (1-1) parallel to $T_1$ and let it intercept the line 1-1.

  3. Set the scaled vector 6.21 on line 3-3 at 2 locations, and call the upper points "a" and "b" respectively.

  4. Draw two lines parallel to $T_2$ and let the lines pass the points "a" and "b", now we get two sets of solutions, which can be more.

enter image description here

r13
  • 7,917
  • 3
  • 8
  • 27
  • 1
    What are the tensions in the three cables according to your approach? – Emmanuel José García Jul 16 '22 at 19:40
  • I've pointed out 3 of the equations required to solve the 3 unknowns. You shall be able to write the equations and solve them. The only thing you need to pay attention to is assigning the +/- sign consistently with the sign convention of your choice. – r13 Jul 16 '22 at 20:11
  • 1
    I think your diagram is wrong because you are assuming that the head of the vector of T2 hangs from the intersection formed by the horizontal line and the vertical line. But the vector head of T2 just hangs from the vertical line. It doesn't touch the ceiling. Sorry for the bad drawing. – Emmanuel José García Jul 16 '22 at 22:02
  • In other words, the heads of the vectors of T1 and T2 do not form a horizontal line. – Emmanuel José García Jul 16 '22 at 22:09
  • No matter what, the third equation must be based on a triangle bounded within two vectors, so you can get the relation between T1 and T2, or T1 and T3. The trick is to work the geometry to get the required information if possible. Otherwise, there is no solution due to inadequate data. – r13 Jul 16 '22 at 22:46
  • The diagram just provides another set of three unknowns, so is not a suitable answer to the question. – PM-14 Jul 16 '22 at 23:02
  • Yes, I now think the solutions are infinite. But I dont get why my equations gave the values I have in my scaled diagram. – Emmanuel José García Jul 17 '22 at 17:33
  • I think it is caused by the fact that the number of unknowns is greater than the available equations, in which, each shall be independent of the others. I'll let you know if I find a more convincing reason. – r13 Jul 17 '22 at 17:51
  • 1
    I suggest posting the question on the mathematics forum, from which you might get a satisfactory answer. This is a very interesting/challenging exercise though. – r13 Jul 17 '22 at 18:08