Submerged fraction buoancy force

Question

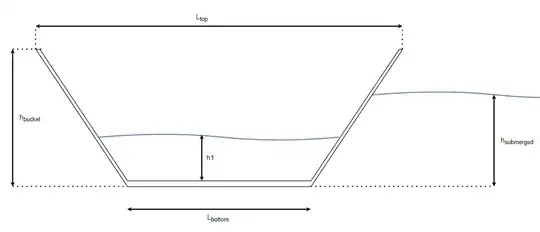
How can I calculate the height of the submerged part of a partly filled bucket? (The liquid both inside and outside is freshwater). The bucket is trapezoidal such that the volume of the submerged can be described as:

<$V_{bucket} = L_{bottom}*L_{bottom}*h_{submerged} + 2 \cdot (\frac{1}{2} \cdot h_{submerged}^2 \cdot (\frac{0.5 \cdot (L_{top}-L_{bottom})}{h_{bucket}}))$>

Can I calculate this using the gravitational force alone (such that I use the mass of the water inside the bucket) as:

<$g \cdot (m_{bucket}+m_{water}) = \rho \cdot g \cdot V_{Liquid} $>

Or should I calculate the force from the water inside using the hydrostatical pressure as:

<$m_{bucket} \cdot g + P_{atm} + \rho \cdot g \cdot h1 = \rho \cdot g \cdot V_{Liquid}$>

Also in relation to the buoyancy force, should I take the angle at the sides into account or do I just use the center of buoyancy?

Thanks

Answer 1

Archimedes' principle states that:

Any object, totally or partially immersed in a fluid or liquid, is buoyed up by a force equal to the weight of the fluid displaced by the object.

In other words; for a body partially submerged, the buoyancy force is equal to the total weight of the body. For a body fully submerged, the buoyancy force is equal to the volume of the body times the density of the fluid it displaces.

---

If applying Archimedes' principle to your problem (a floating/partially submerged body), we know that the weight of the water displaced by the bucket is equal to the total weight of the bucket (including both the actual bucket and the liquid inside). Knowing the weight of the displaced water allows us to calculate the volume of the displaced water, and at last solve for the submerged height.

That is, $$m_{bucket\,including\,liquid}= V_{displaced\,water} * \rho_{displaced\,water}$$ where the unknown is $V_{displaced\,water}$. Then, since the shape of the displaced water volume is given by the shape of the bucket, we have: $$V_{displaced\,water} = V_{bucket}$$ which can be solved for $h_{submerged}$ using the equation described by the question.