What process is involved in freeform 3D tube bending?

Question

I have seen 3D freeform tube bending in videos such as this, this, and this. I would like to ask what process is involved in such machines. I can see a swivel mechanism used for bending. What is it called? How exactly does it work? What is the math involved to back-calculate the CNC code / motion in order for any given shape?

Answer 1

This is just regarding math and springback

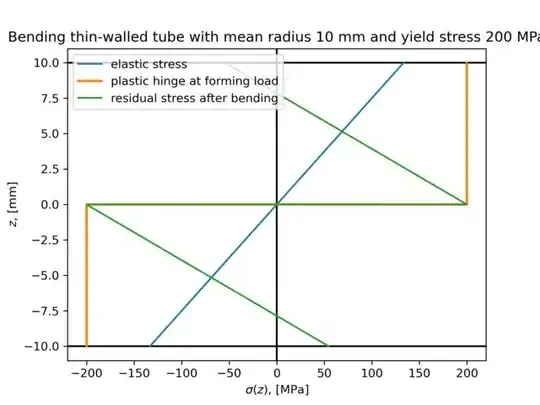
In pure bending, axial strains have a linear distribution through section depending on coordinate $z$ and bend radius $R$:

$$\epsilon(z) = \frac{z}{R}$$

Resulting elastic stress would be simply the strain multiplied by Youngs modulus $E$:

$$\sigma_{el} = E\cdot \frac{z}{R}$$

For bend forming, you need to go into plasticity. Bending with elastoplastic material results in plasticity around elastic core in the section. For bends with relatively small radii, we can assume, that the bending stress at applied loads is fully plastic at yield stress $R_e$:

$$\sigma_{pl} = \begin{cases}R_e & \mathrm{for\;} z>0 \\ -R_e & \mathrm{for\;} z < 0\end{cases}$$

When you remove the loads after going into plasticity, axial strain will go back a little bit with linear distribution through the section $\delta \epsilon = k\cdot z$. So the residual axial stress will be:

$$\sigma_{residual} = \begin{cases}R_e-E\delta\epsilon & \mathrm{for\;} z>0 \\ -R_e-E\delta\epsilon & \mathrm{for\;} z < 0\end{cases}$$

Without the loads, bending moment through the section must be 0, which using symmetry can be written as:

$$\int\limits_0^{z_{max}} z\cdot \left(R_e-E\cdot k\cdot z \right) dA = 0$$

For thinwalled tube with mean radius $r$ and wall thickness $t$, $z = r\cdot \sin(\varphi)$ and $z_{max} = r$:

$$\int\limits_0^{\frac{\pi}{2}} r\cdot \sin(\varphi)\cdot \left(R_e-E\cdot k\cdot r\cdot \sin(\varphi) \right) r\cdot d\varphi = 0$$

From this, you can integrate and end up with expression for $k$ (valid for thin-walled tubes):

$$k = \frac{4R_e}{\pi r E}$$

This constant represents difference between curvature under load and resulting target curvature:

$$k = \frac{1}{R_{load}}-\frac{1}{R_{target}}$$

So if you want to transform straight tube into shape with mean radius $R_{target}$, you need to bend it to mean radius $R_{load} = \frac{1}{1+\frac{1}{R_{target}}}$ first.

This is based on many simplifications, in reality it may be better to determine springback using tests.