I want to define the flow through a top hinge flap gate on an inclined wall. The water can flow out of the bottom of the gate as well as the side and, the top.
I want to have an expression of the flow such that it is dependent on the angle of the hinge. However, I haven't been able to derive that myself. Thus I hope someone here can help me out.
I made an illustration of the gate:
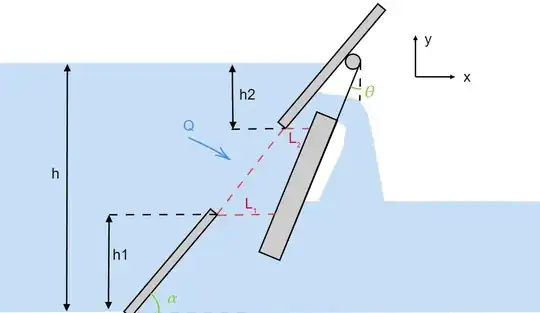
Both upstream and down stream is open to atmospheric pressure and the flow towards the gate can be neglected (only gravity is causing the flow).
So far I've tried to use the orifice equation for the top and bottom as:
$Q_{bottom} = Cd_{bottom} \cdot A_{bottom} \cdot \sqrt{2\cdot g \cdot (h-h_1)}$
$Q_{top} = Cd_{top} \cdot A_{top} \cdot \sqrt{2\cdot g\cdot (h_2)}$
Where the areas are $A_{bottom} = L1 \cdot W$ and $A_{top} = L2 \cdot W$ (W is the width of the gate)
My problem is I don't think this way is the correct one. My thought was if I could define a control volume along the entire flap or something like that. Does anyone have an idea?