How is prestressing with losses self-balanced?

Question

By definition, prestressing is a self-balanced load. This is because it is in fact merely an applied state of internal stresses.

This can also be demonstrated mathematically (in this case for a simple parabolic cable) via Lin's load-balancing method.

For a cable which follows the layout given by $$ y(x) = \dfrac{4e}{L^2}x^2 $$ where $e$ is the vertical distance between the maximum and minimum points of the parabola, $L$ is the span of the cable, and $x=y=0$ is located at the minimum point of the layout, the equivalent load is $$ q = \dfrac{8Pe}{L^2}$$ where $P$ is the prestress force.

Therefore, the total vertical load given by the distributed load is $\dfrac{8Pe}{L}$.

This force is countered by the vertical forces applied at the anchors. These are equal to $P\sin(\theta) \approx P\theta$ and $y'(x) \approx \theta$, so the forces are each equal to $Py'\left(\frac{L}{2}\right) = \dfrac{4Pe}{L}$ and combined are equal (and opposite) to the total distributed load. So the total global load applied is null.

Now, what if we consider friction losses between the cable and the duct in a post-tensioned beam? Then the combined forces at the extremities remain equal to $\dfrac{8Pe}{L}$, but the total distributed load will be reduced by the losses, implying in a non-balanced load, which is impossible.

This may be adjusted by the anchorage slip losses, but what if we assume a hypothetical anchor which doesn't slip? Is this impossible and slippage is necessary to make the load balanced?

And how are the remaining losses (elastic deformation, creep, shrinkage and relaxation) affected?

Answer 1

Comments by @Mr.P nudged me to realize that there is a redistribution of equivalent loads due to losses which cannot be trivially encompassed by Lin's method.

To demonstrate this, take the following simply-supported beam (ignore all concepts of units or scale here, this is a thought exercise).

The bending moment diagram solely due to prestress for this beam will be the following polygonal diagram (before any losses, assuming $P\cos\theta \approx P$):

This is equivalent to the diagram obtained by a concentrated vertical load at midspan equal to $F = 2P\sin\theta \approx 40$, which is balanced out by the two vertical loads at the supports, each equal to $P\sin\theta \approx 20$ (in the opposite direction).

However, let us now consider friction losses. Let's assume they cause a 10% reduction to the stress in the tendon at midspan. This implies that the bending moment at midspan will also be reduced by 10%, and will therefore equal 90. However, the diagram's profile is no longer polygonal.

That can be easily observed by looking at the bending moment at any other point. In an isostatic structure, the bending moment is simply equal to $P \cdot e$, where $e$ is the distance between the cable and the centroid. Looking at quarter-span, the bending moment before losses was equal to $100\cdot0.5=50$, or exactly half of the mid-span moment. To calculate after losses, however, we need to calculate the force at this point. Simplifying things considerably, let's assume the loss here is half of that at midspan, so only 5%.¹ In that case, the bending moment at quarter-span will be equal to $95\cdot0.5=47.5$, which is not equal to half of the mid-span moment of 90.

Indeed, the bending moment diagram from support to midspan becomes of the form

$$M = Pe\left(\dfrac{2x}{L}-0.1\left(\dfrac{2x}{L}\right)^2\right)$$

where $e$ is the distance of the cable to the centroid at midspan, $L$ is the span, and $0.1$ represents the 10% loss of prestress at midspan.

Getting the first and second derivatives of this equation gives us the equivalent concentrated load at midspan and the uniform load distributed along the entire span, respectively:

$$\begin{align} M' = Q &= Pe\left(\dfrac{2}{L} - 0.2\dfrac{4x}{L^2}\right) \\ Q\left(\dfrac{L}{2}\right) &= \dfrac{1.6Pe}{L} \therefore F = 2Q\left(\dfrac{L}{2}\right) = 32 \\ M'' = q &= \dfrac{0.8Pe}{L^2} = 0.8 \end{align}$$

Therefore, the equivalent loading which generates the correct (simplified) bending moment diagram after friction losses is the following:

This implies in a new uniform load which did not appear before losses, a representation of the load redistribution described by @Mr.P. The equivalent concentrated load at midspan is also no longer equal to $F = 2P\sin\theta$, which would have resulted in $F \approx 36$. The prestress, however, is balanced, since $32 + 0.8\cdot10 = 40$, as expected.

---

The same reasoning can be applied to parabolic cables. For the following beam:

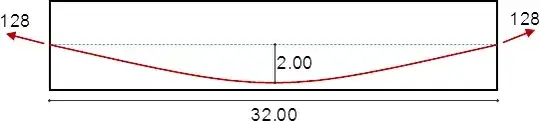
the uniform equivalent load is $q = \dfrac{8Pe}{L^2} = 2$, which generates a total upwards force of $2\cdot32=64$, to be cancelled out by the concentrated downwards forces of 32 at each support. The bending moment diagram before any losses is:

However, assuming once again a 10% loss due to friction at midspan, and that the friction-loss profile is linear, the bending moment diagram becomes:

which has the following cubic equation (with $x=0$ at the midspan):

$$M = 2.00\cdot128\left(1-\left(\dfrac{2x}{L}\right)^2\right)\left(0.9+0.1\dfrac{2x}{L}\right)$$

getting the first and second derivatives, I can find the equivalent loading, which in this case is equal to:

Given what we saw with the first example, it comes as no surprise that there's an increase in the distributed load near the supports. It also makes intuitive sense that the distributed load is reduced near the midspan. How that concentrated load at midspan comes to be, however, I have no idea. However, once again the prestress is self-balanced: $\dfrac{1.8+2.4}{2}\cdot32-3.2=64$.

This answer therefore answers the question posed of how prestressing with losses is self-balanced: the equivalent load is redistributed, but the total value is not modified. That being said, I cannot explain how to calculate this redistribution in a general case because, well, I don't know how that's done.

---

¹ _{Though friction losses are usually quite linear (or polygonal), this is a poor assumption. After all, the 10% loss at midspan must include the effect of the concentrated angle change at that point. At quarter-span, the losses are only due to linear friction loss, and will therefore probably be substantially lower than 5%. That being said, we can just state that 10% is at the point immediately before the angle change, where the bending moment approaches 100 but where only linear friction losses have occurred.}

_{All diagrams obtained with Ftool, a free 2D frame analysis tool.}