7

This might be a stupid question, but I'm new to mechanics, so please bear with me. Suppose I have a compound gearing system defined in the image below (not to scale).

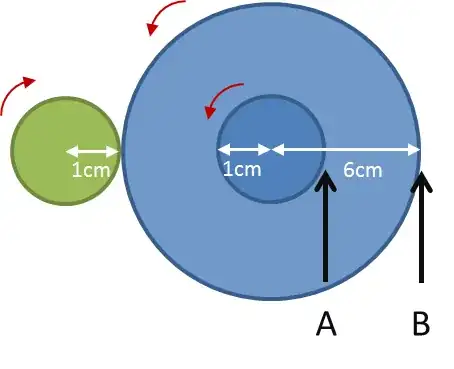
compound gear system

The green gear is the driving gear, and the blue gear is a compound gear.

Suppose I have a driving torque of 10kg.cm, and the ratio is 1:6, this means the output torque is 60kg.cm, correct?

At which point is this torque increase? Is it on the outer edge of the smaller gear (A), or larger gear (B)?

Tom
  • 307
  • 1
  • 7

3 Answers3

4

First, kg-cm is not a unit of torque. On the surface of the earth, your 10 kg-cm would actually be 98 N-cm, or 0.98 Nm. If these gears are on a satellite in space, then kg-cm for torque is completely nonsensical. For sake of example, I'll assume you are relating mass to force by gravity here on the surface of the earth. Please be more careful with units next time. There is no place in engineering for sloppiness with units.

Yes, the 0.98 Nm applied to the left gear would be seen as 6 times that, or 5.9 Nm at the right gear.

This torque exists everywhere on the right gear. Torque is not position-dependent. You can think of torque as the position-independent way of expressing a rotational force. To find the force at a particular point, divide the torque by the radius at that point. For example, at A the force is (5.9 Nm)/(0.01 m) = 580 N. At B the force is (5.8 Nm)/(0.06 m) = 98 N.

Olin Lathrop
  • 11,351
  • 1
  • 20
  • 36
  • Ah, apologies! I've been used to converting N.m to kgf.cm. I guess you helped me out more than I was expecting! Thanks! – Tom Nov 29 '15 at 16:17
  • Am I literally the only person in the world that thinks the kilogram-force is a perfectly good and useful unit of force? – Robbie Mckennie Jan 09 '16 at 21:38
  • @Robb: Go back to high school physics and this time pay attention to what exactly *force* and *mass* are. – Olin Lathrop Jan 09 '16 at 22:14
  • I'm not talking about mass, I'm talking about force. Precisely, the force due to gravity upon one kilogram-mass at sea level on earth. Look it up, kilogram-force is a precedented unit of force. – Robbie Mckennie Jan 09 '16 at 22:36
  • @Robb: The kg is a unit of *mass*. Using it as a unit of force requires some implied acceleration as the conversion factor. If that's not clear, then kg-force is just plain wrong, as in the question here. There was no mention of this being on the surface of the earth. 1 kg-force is a very different value on a satellite in orbit, on the moon, or for a Mars rover, for example. Use Newtons. That's what they are for. Sloppiness with units is not acceptable here. – Olin Lathrop Jan 09 '16 at 23:23
  • It's not sloppy, I just defined it. If you'd wanted to, you could have looked it up and found the definition. It's simply another unit, with a conversion factor of 9.80665. Do you crash discussions taking place using imperial units of distance, and start moaning about how much better the meter is? If so, I feel sorry for you. The kg is a unit of mass, granted, but the kgf is a unit of force, with a clear definition, and indeed much more utility to people living on earth using the metric system than the newton. – Robbie Mckennie Jan 09 '16 at 23:30
  • @Robb: That's the point. If you're going to use a dumbed-down unit for force like kg-force, then you have to define what acceleration you are using. No, you didn't define it, not in your first comment. You only did that after getting called on unit sloppiness. The OP didn't define the acceleration either, which is why I had to make a assumption - and stated so - in this answer. And you can't even get your own conversion factor right! LOL! Clearly it can't be a dimensionless quantity. Duh! What if you were on a lunar base? 9.8 m/s**2 would be a very inconvenient conversion factor. – Olin Lathrop Jan 09 '16 at 23:44
  • Is that a joke? I _did_ define it. "he force due to gravity upon one kilogram-mass at sea level on earth" Doesn't that specify the acceleration clearly enough for you? And like I said, you could have just looked it up if you didn't understand what it meant. Of course a conversion factor can be a dimensionless number, what are you talking about? Are you saying that to be proper it would have to be 9.8 newtons per kgf? Stop being such a pretentious prat. – Robbie Mckennie Jan 10 '16 at 00:18
1

Yes the torque on the driver(green or smaller pinion)would be present on the driven(blue or larger gear) multiplied by the gear ratio i.e. 6 times as much. This torque would be constant over the entire cross section of the driven gear. The rotational force would vary along the cross section inversely with the radius. In contrast the force remains constant across the interface or mesh of the gears( neglecting friction)

PiisTheLimit
  • 31
  • 5
0

I think that the most useful answer to your question is that, in practice we are most concerned about the relative torque between two linked shafts.

To put it another way the forces on gears are only of interest to people who design gears and if you are designing a gearbox it's the ration of torque/RPM which is of primary interest.

In your example shaft Shaft B will see 6x the torque of shaft A and rotate at 1/6 RPM. At this point the diameter of the smaller gear on shaft B is irrelevant until we know what it is coupled to.

Having said that you are correct in saying that the ratio of torque between shaft A and shaft B is 1:6 and the ratio of angular velocity(RPM) is 6:1 ie shaft B has 6 time more torque and rotates at 1/6th of the speed.

For it to be true compound gear train you also need a shaft C coupled t the smaller gear on shaft B.

If the gear on shaft C was 6cm in diameter then you would have a final drive ratio of 1:(6x6) ie 1:36

Chris Johns
  • 15,148
  • 3
  • 21
  • 42