Problem with process controls/simulink?

Question

I have an issue with simulink, basically it's to do with a second order system, well two first order systems in series. As I understand it as you increase the damping factor (above 1), the system should respond slower and be more sluggish. The damping factor = (tau1+tau2)/(2root(tau1*tau2)). So, looking at this system with damping factor 1(with it's response):

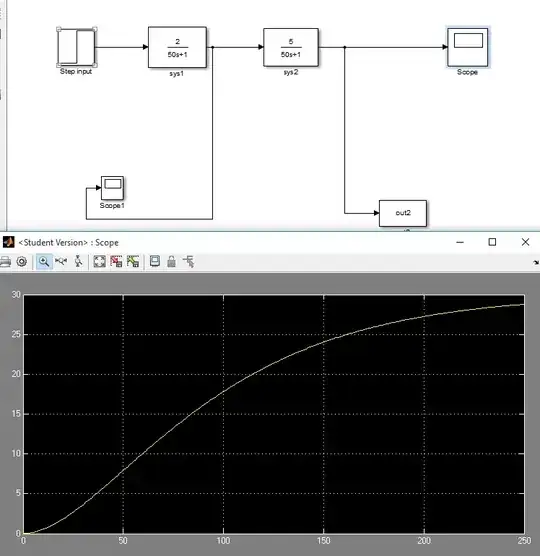
and this system with damping factor 1.19 and it's response:

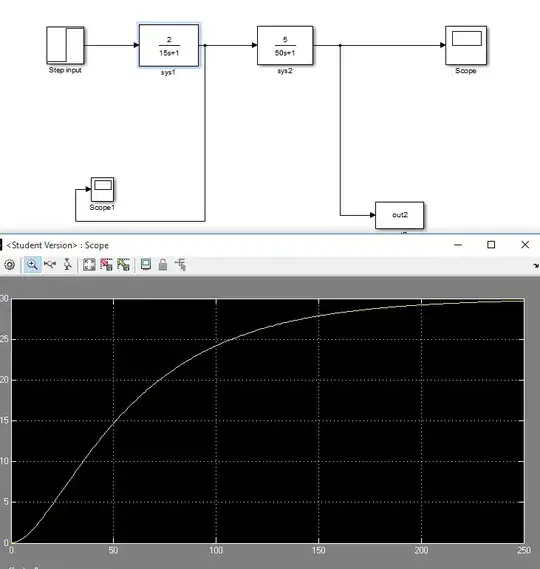
What gives?! The system with the damping factor 1 hasn't even reached steady state by 250 secs while the system with damping factor 1.19 has had a faster response, why is this happening?

Thanks for reading.

Answer 1

Time Constant and systems

A second order LTI system in Laplace domain:

$\hspace{2.5em}$ $H(s) = \frac{{\omega_{n}}^{2}}{s^{2}+\zeta\omega s+{\omega_{n}}^{2}}$

The solution is:

$\hspace{2.5em}$ $h(t) = \frac{{\omega_{n}}}{\sqrt{1-\zeta^{2}}}e^{-\zeta {\omega_{n}} t}sin({\omega_{n}} \sqrt{1-\zeta^{2}}t)$

Note that the time constant depends on the product of the damping and the frequency!

The denominator is called chacateristic equation:

$\hspace{2.5em}$ $s^{2}+\zeta{\omega_{n}} s+{{\omega_{n}}}^{2}$

$\hspace{2.5em}$ $r_{1,2} = \frac{-\zeta{\omega_{n}}\pm \omega_{n}\sqrt{1-\zeta^{2}}}{2}$

We have three forms for the solution:

Overdamped: $r_{1} \neq r_{2}$ $\in$ $\Re$

Critically damped: $r_{1} = r_{2}$ $\in$ $\Re$

Underdamped: $ r_{1} = {r_{2}}^{*}$. Where ${r_{2}}^{*}$ is the complex conjugate of $r_{1}$

In the s plane, should look like this:

The figure above show us a complex response (the conjugate is implicated). Note that $-\zeta\omega_{n}$ its in the real part of the solution! So, is responsible for the time response and, the imaginary part, $\omega_{n}\sqrt{1-\zeta^{2}}$ is responsible for the oscilation.

Note that the real part is the exponential term in the solution!