Important note: I am writing a structural FEM software from scratch, so I won't able to use existing commercial FEM package. I would need to know how all the important quantities are calculated from the first principles.
I would need to determine the accidental torsional effect ( UBC97, 1631.5.6, pp-27, this accidental torsion effect is needed for both response spectrum and linear time history analysis) for seismic dynamic analysis.
$M_t=F_xe_y$
Where
$F_x$ is the equivalent lateral static force in $x$ direction
$e_y$ is the accidental eccentricities in $y$ direction
Take note that all these involved quantities are evaluated on floor basis.
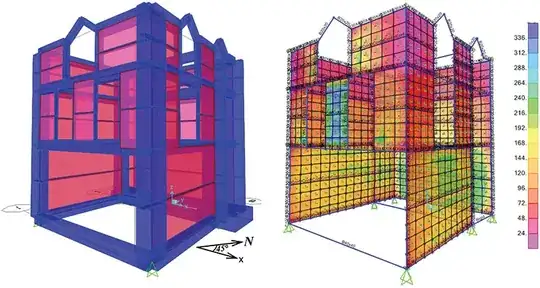
My structures are quite irregular and general, such as this:
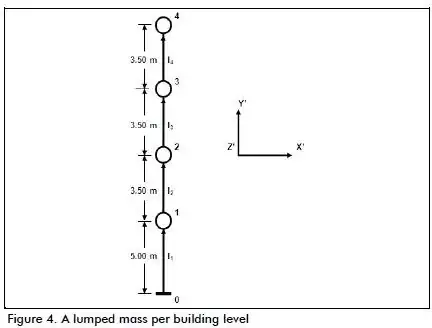
For a cantilever column or an one dimensional lumped mass model, the term on floor basis is easy to interpret because there is only 1 node per floor, and the $F_x$ can only be applied on this node itself. Compare this lumped mass model with the above 2D structure FEM model and you can see the difference:
But when you have such a 2 dimensional irregular structure, analyzed using FEM, calculating $F_x$ and $M_t$ is no longer easy:
- How should we obtain $F_x$, given that it is lateral static force, but we are doing dynamic analysis?
- There are so many nodes on a floor, so on which node(s) should the $M_t$ be applied?
- In FEM, each beam, column, wall and slab are multiple-node elements. And each node has a internal force value resulted from FEM analysis, what should I do with all these forces at different nodes? The comment here says that I should sum up all of the forces on each related node in order to obtain the correct $F_x$ ( I'm not sure whether I interpret it correctly or not). But I am highly skeptical of this approach, because won't that make $F_x$ dependent on the number of nodes, an artifact of how we mesh an element? How can a real physical quantity increases with the number of nodes we decide to mesh?
- If 3) is true, then what about the $F_x$ on the wall above a particular floor? Should we sum them in? What about the internal slab and beam? Do they have this force also?
- How should we intepret $M_t$? Is it internal member force to be resisted by beam/slab? If yes, if there are many slabs and beams into $x$ direction, then how should this $M_t$ be distributed? Or is it an external static force; so one would have to apply this external force on the structure in order to calculate the individual internal member force induced by it ( via the FEM equation $ku=F$)?
So the question is, how to calculate and interpret accidental torsion in a FEM model? I've tried to obtain a general way to reduce a 2 Dimensional general FEM structure into 1 Dimensional lumped mass model, so that I can apply the above formulation easily, but I was told that this wasn't possible.