3

I know ROC curve always looks like a stair shape and that I can evaluate AUC of ROC. And I know I can compute AUC of ROC curve to compare which model is better. What I wonder is:

  • Does precision-recall curves have a constant shape/pattern?
  • Can I compute AUC of PR curve to compare which model is better?
  • If not, how can you compare models by PR curves?
Simon Larsson
  • 4,083
  • 1
  • 14
  • 29
disney82231
  • 97
  • 1
  • 7

2 Answers2

1

I wonder if PR curve(Precision-Recall curve) has a constant shape(pattern)?

For a model that is better than random (having a ROC above tpr = fpr line), which is mostly the case, precision and recall roughly have an inverse relationship. Therefore, we should expect that a (precision, recall) curve generally decreases (checkout this post on the relationship between precision and recall).

Can I compute AUC of PR curve to compare which model is better?

Yes. It is even preferred over AUC (of ROC) when classes are imbalanced in the test set (for example, check out this blog, this Kaggle notebook, and this 2015 paper). Here is an image from the referenced blog

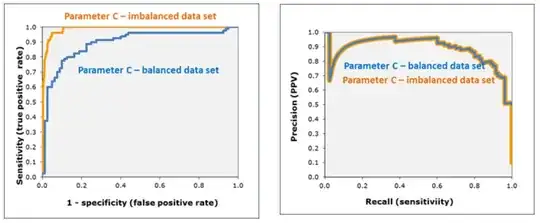
enter image description here

which shows that PRC (right), unlike ROC (left), is robust to imbalanced classes.

And here is a quote from the referenced Kaggle notebook (texts in brackets are added by me):

ROC curve is not a good visual illustration for highly imbalanced data, because the False Positive Rate ( False Positives / Total Real Negatives ) does not drop drastically [i.e., does not produce a lower curve with smaller AUC] when the Total Real Negatives is huge [i.e., negative class is much larger than positive class].

Whereas Precision ( True Positives / (True Positives + False Positives) ) is highly sensitive to False Positives and is not impacted by a large total real negative denominator.

which is illustrated as below

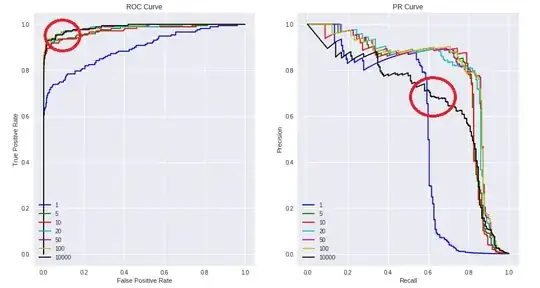
enter image description here

emphasizing on the black model (black curve) that is shown to be powerful in ROC but not that much in PRC; given that negative to positive ratio is around 600 (the ratio should be 1 when classes are balanced).

Esmailian
  • 9,147
  • 2
  • 31
  • 47
0

The perfect PR curve is upper right hand corner. You can compute compute the AUC of PR curve to compare models, and similar to an AUROC, a higher AU the PR curve would be better. Another option would be to choose a cutoff and compare methods there.

http://www.chioka.in/differences-between-roc-auc-and-pr-auc/

Leo Brueggeman
  • 143
  • 6