How to interpret the phase plot from an accelerometer on vibrating machinery

Question

Attached is a plot of amplitude vs frequency and on the inset phase vs frequency. I have constructed this phase plot via $\arctan\left(\frac{Im}{Re}\right)$

How can I interpret the phase plot or extract some meaningful info from it, particularly in the region of the almost vertical line? This line occurs at around 102Hz which is nowhere near the amplitude peaks.

Answer 1

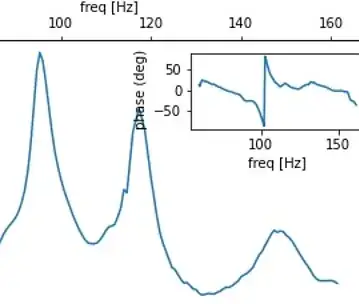
I'm not an expert, but that vertical line in the phase is usually when transitioning over a critical rotational velocity of a shaft.

This happens when the excitation frequency "transverses" the critical frequency of the shaft. The displacement of the shaft can be derived for an ideal motor (no damping):

$$ y = \frac{e\cdot \omega^2}{\omega_n^2 - \omega^2} = \frac{e}{\frac{\omega_n^2}{ \omega^2} - 1} $$

while a more advanced approach, with the inclusion of damping, calculates the dynamic magnifier as :

$$H(r,\zeta) = \frac{r^2}{\sqrt{(1-r^2)^2 + (2\zeta r)^2}}$$

the phase angle can be estimated by a similar expression as:

$$\phi = \arctan\left(\frac{2\zeta r}{1- r^2}\right)$$

where:

• $\zeta$: is the damping ratio
• $r=\frac{\omega}{\omega_n}$

So when passing through the natural frequency $\omega_n$ what happens is that :

• (usually )you get a maximum value of the displacement
• you get an inversion of the phase angle $\phi$ (the ratio becomes greater than 1).

So what you are seeing in this graph at about 115[Hz]$\approx 6900rpm$, is that you pass through the critical speed of the shaft.

The earlier peak (at about 95Hz) is probably another natural frequency of the engine assembly.